删除二叉搜索树中的节点(面试常见题)

末蓝、 2022-10-23 08:27 142阅读 0赞

# 一、题目描述 #

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；  
如果找到了，删除它。

**说明：** 要求算法时间复杂度为 O(h)，h 为树的高度。

**示例**：

root = [5,3,6,2,4,null,7]
    key = 3
    
        5
       / \
      3   6
     / \   \
    2   4   7
    
    给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
    
    一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
    
        5
       / \
      4   6
     /     \
    2       7
    
    另一个正确答案是 [5,2,6,null,4,null,7]。
    
        5
       / \
      2   6
       \   \
        4   7

# 二、思路分析 #

想要删除某个结点，首先要**定位**到这个结点：

二叉搜索树的数据域是有序的：

*  二叉搜索树左子树上所有结点的数据域都小于等于根结点的数据域
 *  二叉搜索树右子树上所有结点的数据域都大于等于根结点的数据域
 *  **左孩子 <= 根结点 <= 右孩子**
 *  利用二叉搜索树数据域的有序性可以快速定位节点

**val<当前节点值：往左走；val>当前节点值：往右走**

找到这个结点后，就要进行**删除**操作了：

*  定位到了空结点，直接返回即可
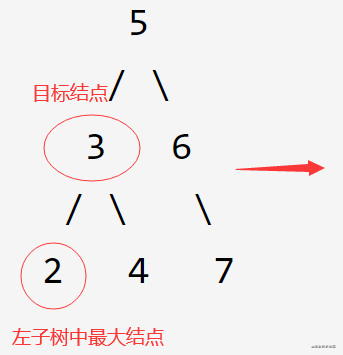
 *  目标结点是一个叶子结点，直接删除即可
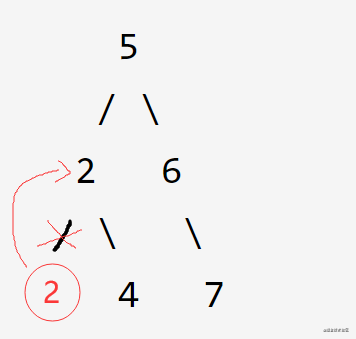
 *  目标结点存在左子树，用其左子树里的最大结点覆盖掉目标结点
 *  目标结点存在右子树，用其右子树里的最小结点覆盖掉目标结点
 *  目标结点既有左子树、又有右子树，从前面左节点或右节点的方法中取一执行即可

这样操作完之后仍能维持二叉搜索树的数据有序性。

![c8b32c70601bd70f176e501839cc608a.png][]![e54ff67bf60c145cec61ef872847606d.png][]

# 三、AC 代码 #

/**
     * Definition for a binary tree node.
     * function TreeNode(val, left, right) {
     *     this.val = (val===undefined ? 0 : val)
     *     this.left = (left===undefined ? null : left)
     *     this.right = (right===undefined ? null : right)
     * }
     */
    /**
     * @param {TreeNode} root
     * @param {number} key
     * @return {TreeNode}
     */
    function deleteNode(root, n) {
        // 如果没找到目标结点则直接返回
        if(!root) {
            return root
        }
        // 找到目标结点，开始分情况进行删除
        if(root.val === n) {
            // 若是叶子结点，直接设为null
            if(!root.left && !root.right) {
                root = null
            } else if(root.left) {
                // 寻找左子树里值最大的结点
                const maxLeft = findMax(root.left)
                // 用左子树里值最大的结点覆盖掉需要删除的当前结点  
                root.val = maxLeft.val
                // 删掉原有maxLeft 结点
                root.left = deleteNode(root.left, maxLeft.val)
            } else {
                // 寻找右子树里值最小的结点
                const minRight = findMin(root.right)
                // 用右子树里值最小的结点覆盖掉需要删除的当前结点  
                root.val = minRight.val
                // 删掉原有minRight 结点
                root.right = deleteNode(root.right, minRight.val)
            }
        } else if(root.val > n) {
            // 若当前结点的值比 n 大，在左子树中寻找目标结点
            root.left = deleteNode(root.left, n)
        } else  {
            // 若当前结点的值比 n 小，在右子树中寻找目标结点
            root.right = deleteNode(root.right, n)
        }
        return root
    }
    
    // 寻找左子树最大值
    function findMax(root) {
        while(root.right) {
            root = root.right
        }
        return root 
    }
    
    // 寻找右子树的最小值
    function findMin(root) {
        while(root.left) {
            root = root.left
        }
        return root
    }

# 四、总结 #

*  删除的时候需要考虑如何维持二叉搜索树的**数据有序性**。

[文章链接：https://juejin.cn/post/6937639546888667173/][https_juejin.cn_post_6937639546888667173]

[c8b32c70601bd70f176e501839cc608a.png]: https://img-blog.csdnimg.cn/img_convert/c8b32c70601bd70f176e501839cc608a.png
[e54ff67bf60c145cec61ef872847606d.png]: /images/20221023/39b1a800109e4f4aae3ee8185b1d2a10.png
[https_juejin.cn_post_6937639546888667173]: https://juejin.cn/post/6937639546888667173/