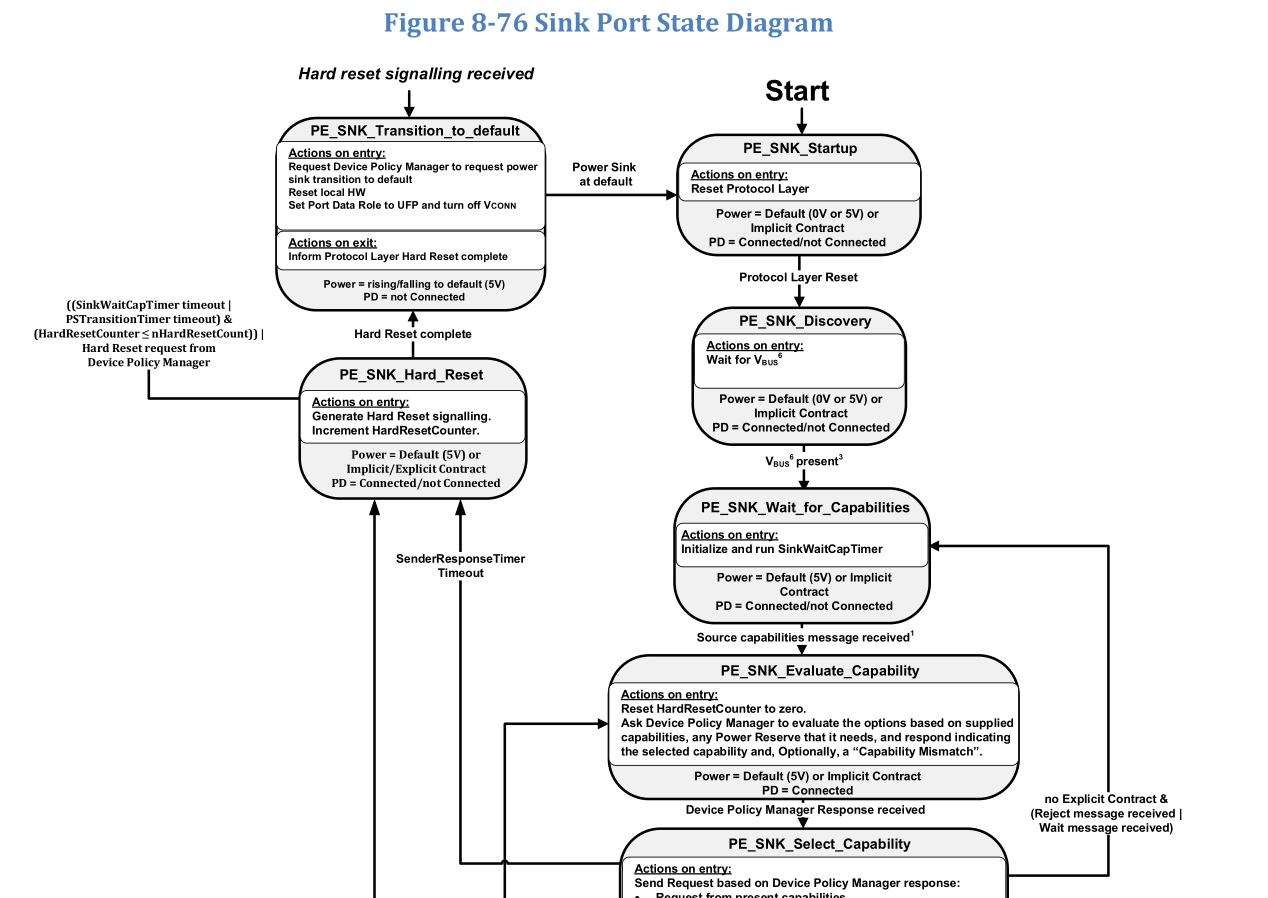
count color线段树java_Count Color POJ - 2777 线段树-蒲公英云

count color线段树java_Count Color POJ - 2777 线段树

Chosen Problem Solving and Program design as an optional course, you are required to solve all kinds of problems. Here, we get a new problem.

There is a very long board with length L centimeter, L is a positive integer, so we can evenly divide the board into L segments, and they are labeled by 1, 2, … L from left to right, each is 1 centimeter long. Now we have to color the board - one segment with only one color. We can do following two operations on the board:

“C A B C” Color the board from segment A to segment B with color C.
“P A B” Output the number of different colors painted between segment A and segment B (including).

In our daily life, we have very few words to describe a color (red, green, blue, yellow…), so you may assume that the total number of different colors T is very small. To make it simple, we express the names of colors as color 1, color 2, … color T. At the beginning, the board was painted in color 1. Now the rest of problem is left to your.

Input

First line of input contains L (1 <= L <= 100000), T (1 <= T <= 30) and O (1 <= O <= 100000). Here O denotes the number of operations. Following O lines, each contains “C A B C” or “P A B” (here A, B, C are integers, and A may be larger than B) as an operation defined previously.

Output

Ouput results of the output operation in order, each line contains a number.

Sample Input

2 2 4

C 1 1 2

P 1 2

C 2 2 2

P 1 2

Sample Output

线段树

用一个LL 位表示颜色情况

用一个laz表示当前块是否是同一颜色的

pushdown

如果当前颜色是统一的，那么将这个颜色推给下面，同时将下面的laz标识设置为1，然后清除该标识

pushup

color是左右子节点color的按位与

如果左边颜色是统一的！而且右边颜色是统一的！而且左右两边颜色相同！

才讲该节点的laz设置为1

在查询的时候由于我们查询的是color，如果当前区间的laz = 1

表示区间内所有颜色都是统一的，那么我们可以直接返回当前节点的颜色

#include#include#include#include

using namespacestd;

typedeflong longLL;#define MAXN 100009LL l,t,o;structnode

{

LL l,r;

LL laz;

LL sum;//用一个数字的每个位表示这个段有多少颜色

}T[MAXN * 5 + 3];voidpushdown(LL p)

{if(T[p].laz)

{

T[p].laz= 0;

T[p*2].laz = T[p*2+1].laz = 1;

T[p*2].sum = T[p*2 +1 ].sum =T[p].sum;

}

}voidpushup(LL p)

{

T[p].sum= T[p*2].sum | T[p*2+1].sum;if(T[p*2].laz && T[p*2+1].laz && T[p*2].sum == T[p*2 +1].sum)

T[p].laz= 1;

}voidbuild(LL x,LL l,LL r)

{

T[x].l= l,T[x].r =r;if(l ==r)

{return;

}

LL mid= (l + r)/2;

build(x* 2,l ,mid);

build(x* 2 + 1,mid + 1,r);//pushup(x);

}voidupdate(LL x,LL l,LL r,LL val)

{if(T[x].l == l&&T[x].r ==r)

{

T[x].sum= ( 1<< (val - 1) );

T[x].laz= 1;return;

}

pushdown(x);

LL mid= ( T[x].l + T[x].r)/2;if(r<=mid)

update(x* 2, l ,r, val);else if(l >mid)

update(x*2 +1, l , r, val);else{

update(x* 2,l, mid,val);

update(x* 2 + 1,mid + 1, r, val);

}

pushup(x);

}

LL query(LL x, LL l, LL r)

{if(T[x].laz || (T[x].l == l && T[x].r ==r))

{returnT[x].sum;

}//pushdown(x);

LL mid = (T[x].l + T[x].r )/2;if(r<=mid)return query(x * 2, l, r);else if( l >mid)return query(x * 2 + 1, l ,r);else{//LL tmp1 = query(x *2, l, mid);//LL tmp2 = query(x*2 +1, mid + 1, r);

return query(x *2, l, mid) | query(x*2 +1, mid + 1, r);

}

}intmain()

{char c[2];

LL L,R,tmp;

scanf(“%lld%lld%lld”,&l,&t,&o);

build(1,1,l);

T[1].laz = T[1].sum = 1;for(LL i = 0;i

{

scanf(“%s%lld%lld”,c,&L,&R);if(L >R)

{

LL sd=L;