二叉树的先序遍历中序遍历后序遍历层序遍历-蒲公英云

二叉树的先序遍历中序遍历后序遍历层序遍历

快来打我* 2023-01-10 14:39 371阅读 0赞

两种特殊的二叉树

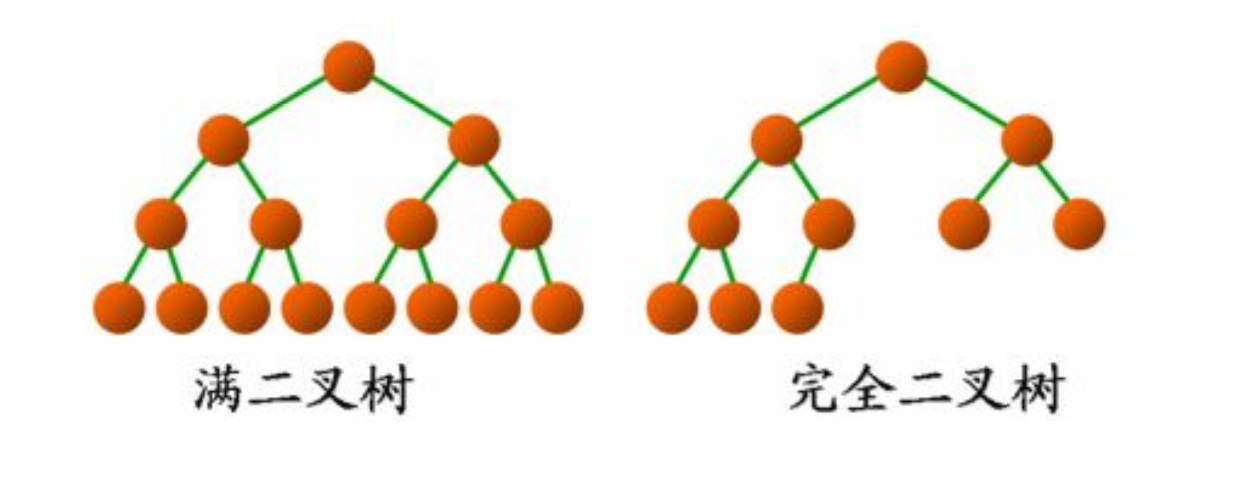
完全二叉树: 完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

满二叉树: 一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树

在这里插入图片描述

二叉树的遍历

先序遍历：先遍历根节点，再遍历左节点，最后遍历右节点

中序遍历：先遍历左节点，再遍历右节点，最后遍历根节点

后序遍历：先遍历左节点，再遍历右节点，最后遍历根节点

层序遍历：自上而下，自左至右逐层访问树的结点的过程就是层序遍历

遍历方法的实现

先建立一棵树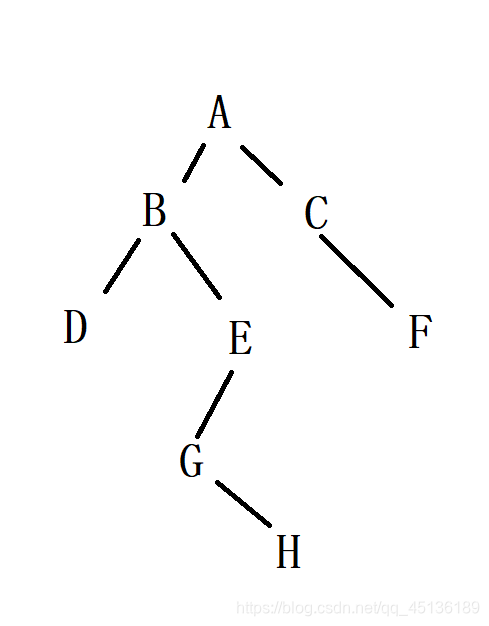
在这里插入图片描述
用代码建立以上树

class Node {
    public char val;
    public Node left;
    public Node right;
    public Node(char val) {
        this.val = val;
    }
}
public class TestTree {
    public static Node build(){
        //手动把一颗树构造出来
        Node a = new Node('A');
        Node b = new Node('B');
        Node c = new Node('C');
        Node d = new Node('D');
        Node e = new Node('E');
        Node f = new Node('F');
        Node g = new Node('G');
        Node h = new Node('H');
        a.left = b;
        a.right = c;
        b.left = d;
        b.right = e;
        e.left = g;
        g.right = h;
        c.right = f;
        //返回根节点
        return a;
    }
}

下面进行先序遍历：

//先序遍历
    public static void preOrder(Node root){
        if (root == null){
            return;
        }
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

下面进行中序遍历

//中序遍历
    public static void inOrder(Node root){
        if (root == null){
            return;
        }
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }

下面进行后序遍历

//后序遍历
    public static void postOrder(Node root){
        if (root == null){
            return;
        }
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val+" ");
    }

下面进行层序遍历

//层序遍历
    public void levelOrder(TreeNode root){
        //不能使用递归
        //可以借助一个队列来完成
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);//先把根入队列
        while (!queue.isEmpty()){
            TreeNode cur = queue.poll();//去队首元素
            //访问数据
            System.out.println(cur.val+" ");
            //把左右子树入队列
            if (cur.left != null){
                queue.offer(cur.left);
            }
            if (cur.right != null){
                queue.offer(cur.right);
            }
        }
    }

（层序遍历无法使用递归的方法）

补充（非递归实现先序/中序/后续遍历）

import java.util.Stack;
class Node{
    public int val;
    public Node left;
    public Node right;
    public Node(int val) {
        this.val = val;
    }
}
public class TreeNode {
    // 二叉树的前序遍历，非递归迭代实现
    public static void preOrderByLoop(Node root){
        if (root == null){
            return;
        }
        Stack<Node> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            Node top = stack.pop();
            System.out.println(top.val + " ");
            //把右子树和左子树分别入栈
            if (top.right != null){
                stack.push(top.right);
            }
            if (top.left != null){
                stack.push(top.left);
            }
        }
    }
    // 二叉树的中序遍历，非递归迭代实现
    public static void inOrderByLoop(Node root){
        if (root == null){
            return;
        }
        Stack<Node> stack = new Stack<>();
        Node cur = root;
        while (true){
            //1,循环往左找，把路径上遇到的节点都入栈
            while (cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            //2.如果当前栈为空，遍历就结束了
            if (!stack.isEmpty()){
                break;
            }
            Node top = stack.pop();
            System.out.println(top.val + " ");
            cur = top.right;
        }
    }
    // 二叉树的后序遍历，非递归迭代实现
    public static void postOrderByLoop(Node root){
        if (root == null){
            return;
        }
        Stack<Node> stack = new Stack<>();
        Node cur = root;
        //prev表示记录了当前已经访问过的节点中的最后一个节点（即将被访问的元素的前一个结点）
        Node prev = null;
        while (true){
            //1,循环往左找，把路径上遇到的节点都入栈
            while (cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            //2.如果当前栈为空，遍历就结束了
            if (!stack.isEmpty()){
                break;
            }
            //拿出栈顶元素的值
            Node top = stack.peek();//拿出来看看
            if (top.right == null || prev == top.right){
                System.out.println(top.val + " ");
                stack.pop();//出栈
                prev = top;//时刻维护好prev指向已经遍历完元素的最后一个
            }else {
                cur = top.right;
            }
        }
    }
}