降维（Dimensionality Reduction）
目录
- 目标 I：数据压缩
- 目标Ⅱ：可视化
- 主成分分析问题规划1
- 主成分分析问题规划2
- 主成分数量选择
- 压缩重现
- 应用.PCA.的建议
目标 I：数据压缩
数据压缩使得的数据占用空间变小，还能对学习算法进行加速。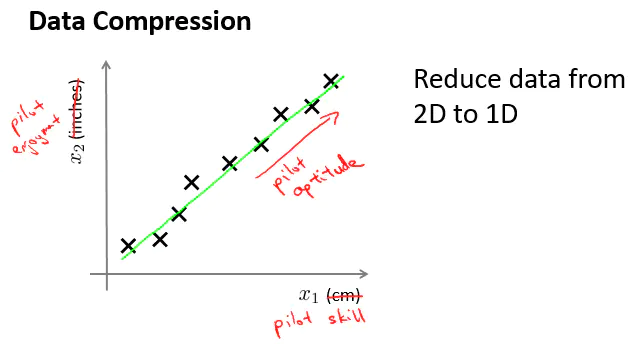
特征之间高度相关。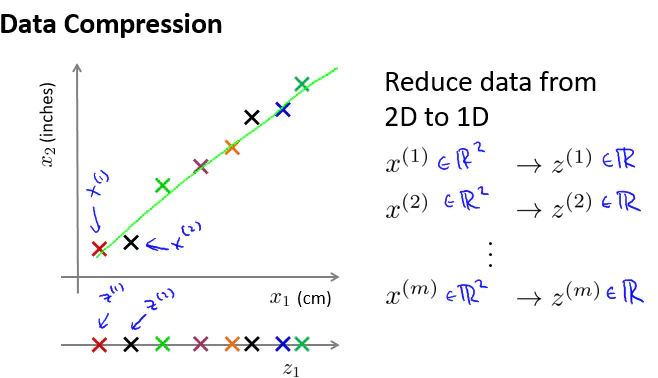
这些数据大概分布在一个平面。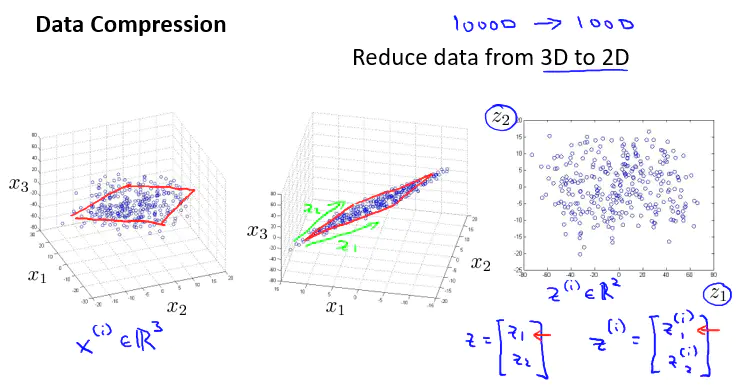
目标Ⅱ：可视化
降维的另一个应用：使数据可视化。
假设我们有50个维度的特征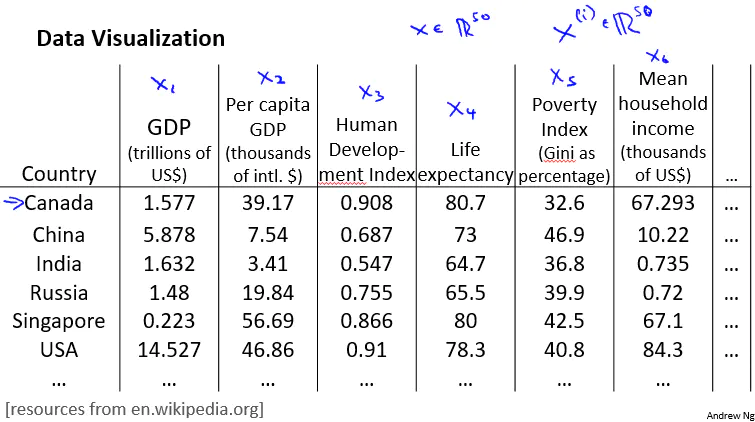
现在降到2维，但是我们常要弄清出降维后的特征大概代表什么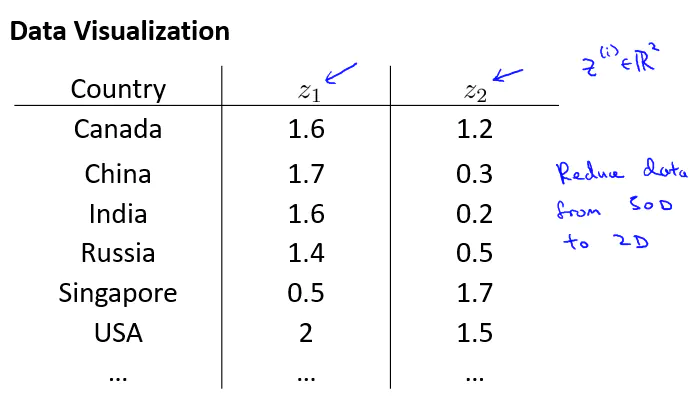
通过降维后观察可视化图像，可知降维后的特征大概代表什么
主成分分析问题规划1
主要成分分析（PCA）方法：
PCA就是想要找到一个低维平面，在下面的例子是一条直线，然后将数据投影在上面，使这些蓝色小线段（投影误差）长度平方最小。
在应用PCA之前常规的做法是先进行均值归一化和特征规范化，使得特征量之间的均值为0，并且其数值在可比较的范围内。
正式写一下PCA问题：
PCA做的就是，如果想将数据从N维降到K维，我们需要寻找K个方向（向量）对数据进行投影，来最小化投影误差。
另外PCA不是线性回归：
线性回归求的是y方向上的最小值，PCA求的是点到投影点的距离最小值。
对所有特征同等对待：
主成分分析问题规划2
在进行PCA之前，应先预处理数据，均值归一化或特征缩放。
如何计算 u 和 z 呢？
PCA具体过程：
①计算协方差（Σ）
②计算 Σ 的特征向量：
在Octave中，用 [U,S,V] = svd（Σ），svd 代表奇异值分解，（在Octave中，用 eig（Σ） 也能计算，虽然有一点别的差别，但是结果相同），在输出的 3 个矩阵中，我们需要的是 U（U 是n*n的矩阵，它的列就是我们需要的向量u(i)，需要降成 k 维，就取前 k 列）。
③获取 U 矩阵的前 k 列，取得的降维后的矩阵叫做 Ureduce
④降维后的新特征，Z = UreduceTX
总之，这是PCA算法：
进行均值归一化后，为确保每一个特征都是均值为0的任选特征缩放，你能够做特征的缩放是，你的特征能够呈现不同范围的值。
预处理完之后，我们计算这个载体矩阵 Σ 。
然后得到U，取出前要降维矩阵的前 k 列，Ureduce 。
最后计算降维后的特征 Z 。
主成分数量选择
假设 K 从 1 开始，直到计算出来式子（平均投影误差的平方除以数据的总方差，它的结果为数据的波动程度，波动越小越好）的值满足要求，我们就选择该 K 的值。
另外的说法就是有多少方差性被保留。
实现算法：
第一种是左边的依次计算。
第二种是右边在Octave中，利用 S 矩阵计算，该方式更加高效。
总结，通过报告方差被保留的百分比，更易理解降维后的数据是如何逼近原始数据的。
压缩重现
把降维的数据还原回原理维度的数据会有损失。
因为还原后的数据只是原来数据的投影，所以具有误差。
应用.PCA.的建议
PCA可以减少硬盘存储空间、提高算法的速度，如果是降到2或3维，还可以可视化。
下面的是提高算法速度：
PCA只运用在训练集，不用在交叉验证集和测试集。
PCA主要应用：
数据压缩，加快算法速度，可视化…
误用：
使用PCA降维去避免过拟合，这是一种不好的做法，不建议这样做（虽然也可以），我们可以使用正则化更好的避免过拟合。
PCA会舍掉一些信息，它扔掉或减少数据的维度，不关心 y 的值是什么，所以它可能会丢掉一些有价值的信息。
在实现PCA之前，首先建议直接做你想做的事，首先考虑原始数据，只有这么做达不到目的的情况下，才考虑使用PCA，或者数据的维数很大，算法运行太慢，占用很多空间和内存，才需要去考虑。
雨点打透心脏的1/2处
港控/mmm°
今天药忘吃喽~
红太狼
灰太狼
还没有评论，来说两句吧...