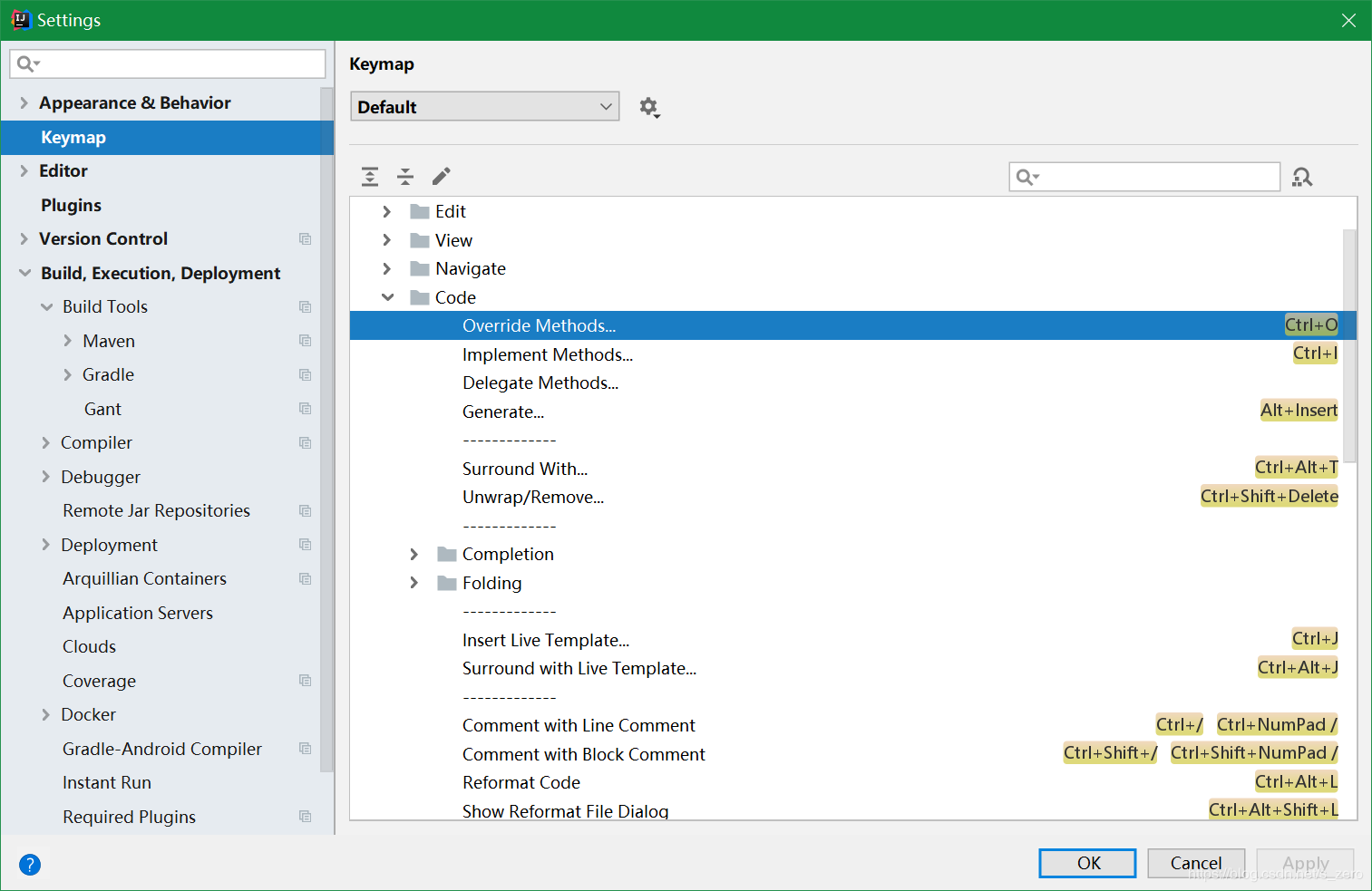
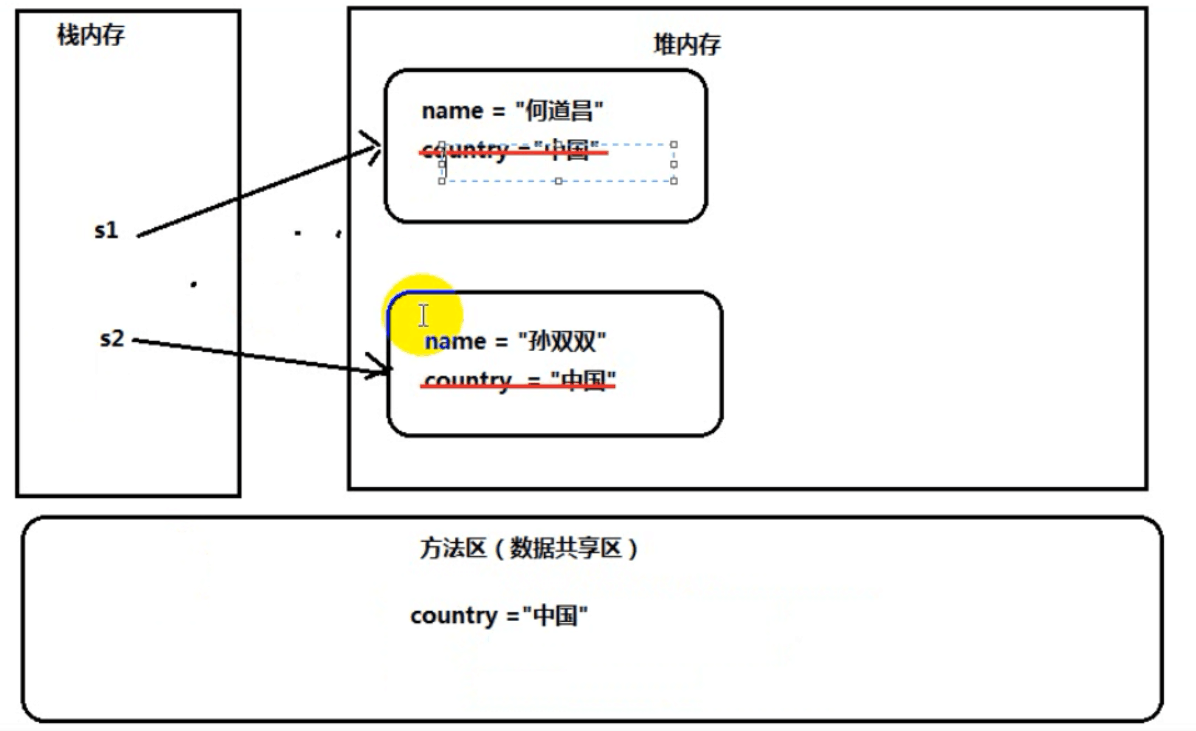
傅里叶变换 二维离散傅里叶变换（代码和性能的优化）

迈不过友情╰ 2023-06-13 03:28 92阅读 0赞

1、一维DFT和二维DFT。

一维DFT公式：

  1. ![F(u)=\\sum\_\{x=0\}^\{N-1\}f(x)e^\{-\\frac\{2\\pi ux\}\{N\}i\}][F_u_sum_x_0_N-1_f_x_e_-_frac_2_pi ux_N_i]。

二维DFT公式：

  1. ![F(u,v)=\\sum\_\{x=0\}^\{M-1\}\\sum\_\{y=0\}^\{N-1\}f(x,y)e^\{-2\\pi (\\frac\{ux\}\{M\}+\\frac\{vy\}\{N\})i\}=\\sum\_\{x=0\}^\{M-1\}(\\sum\_\{y=0\}^\{N-1\}f(x,y)e^\{-2\\pi (\\frac\{vy\}\{N\})i\})e^\{-2\\pi (\\frac\{ux\}\{M\})i\}][F_u_v_sum_x_0_M-1_sum_y_0_N-1_f_x_y_e_-2_pi _frac_ux_M_frac_vy_N_i_sum_x_0_M-1_sum_y_0_N-1_f_x_y_e_-2_pi _frac_vy_N_i_e_-2_pi _frac_ux_M_i]。

可以看作M行N列的二维

发表评论

表情：
评论列表 （有 0 条评论，92人围观）

还没有评论，来说两句吧...

相关阅读

    相关 傅里叶变换

    > 傅立叶变换，表示能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换

    - 日理万妓- 日理万妓/ 0 赞/ 514 阅读