傅里叶变换 二维离散傅里叶变换

待我称王封你为后i 2023-05-30 06:01 326阅读 0赞

1、介绍。

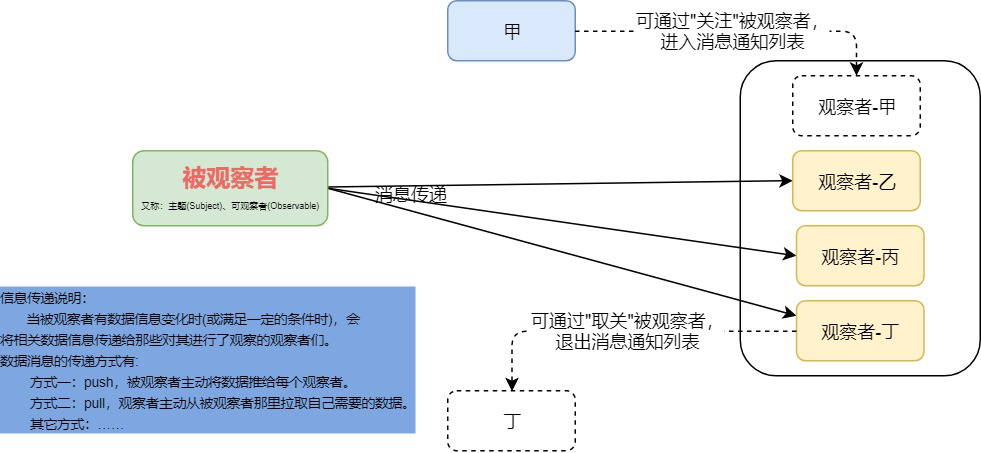
  1.     DFT:(Discrete Fourier Transform)离散傅里叶变换是傅里叶变换在时域和频域上都呈离散的形式，将信号的时域采样变换为其DTFT的频域采样。在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT，也应当将其看作其周期延拓的变换。

1）、欧拉公式：

\\LARGE \\dpi\{100\} \\LARGE e^\{\\theta i\}=cos \\theta +(sin \\theta )i，其中i是虚数，即i的平方为-1。

2）、二维离散傅里叶变换DFT公式：

N是二维数组的行数，M是二维数组的列数。u和v是转换后二维数组的位置，F(u,v)是转换后数组中相应位置的值。x和y是原二维数组的位置，f(x,y)是原数组中相应的值。

发表评论

表情：
评论列表 （有 0 条评论，326人围观）

还没有评论，来说两句吧...

相关阅读

    相关 傅里叶变换

    > 傅立叶变换，表示能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换

    - 日理万妓- 日理万妓/ 0 赞/ 495 阅读

    相关 傅里叶变换

    作 者：韩 昊 知 乎： Heinrich 微 博： @花生油工人 知乎专栏：与时间无关的故事   谨以此文献给大连海事大学的吴楠老师，柳晓鸣老师，王新年老师以及张晶

    梦里梦外;梦里梦外;/ 0 赞/ 462 阅读