LeetCode——动态规划：斐波那契数列

斐波那契数列

public int climbStairs(int n) {
        if (n == 1) {
            return 1;
        }
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
public int climbStairs2(int n) {
        if (n <= 2) {
            return n;
        }
        int pre2 = 1;
        int pre1 = 2;
        for (int i = 3; i <= n; i++) {
            int cur = pre1 + pre2;
            pre2 = pre1;
            pre1 = cur;
        }
        return pre1;
    }

2. 强盗抢劫

在这里插入图片描述
题目描述：抢劫一排住户，但是不能抢邻近的住户，求最大抢劫量。

定义 dp 数组用来存储最大的抢劫量，其中 dp[i] 表示抢到第 i 个住户时的最大抢劫量。
由于不能抢劫邻近住户，如果抢劫了第 i -1 个住户，那么就不能再抢劫第 i 个住户，所以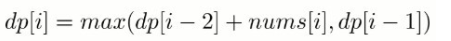
在这里插入图片描述

public int rob(int[] nums) {
        int pre2 = 0, pre1 = 0;
        for (int i = 0; i < nums.length; i++) {
            int cur = Math.max(pre2 + nums[i], pre1);
            pre2 = pre1;
            pre1 = cur;
        }
        return pre1;
    }

3. 强盗在唤环形街区抢劫

https://leetcode-cn.com/problems/house-robber-ii
在这里插入图片描述
题目描述：你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

public int rob(int[] nums) {
        if (nums == null || nums.length == 0) {
            return 0;
        }
        int n = nums.length;
        if (n == 1) {
            return nums[0];
        }
        return Math.max(rob(nums, 0, n - 2), rob(nums, 1, n - 1));
    }
    private int rob(int[] nums, int first, int last) {
        int pre=0,cur=0,tmp;
        for (int i = first; i <= last; i++) {
            tmp = cur;
            cur = Math.max(cur,pre+nums[i]);
            pre = tmp;
        }
        return cur;
    }

4. 信件错排

题目描述：定义一个数组 dp 存储错误方式数量，dp[i] 表示前 i 个信和信封的错误方式数量。假设第 i 个信装到第 j 个信封里面，而第 j 个信装到第 k 个信封里面。

根据 i 和 k 是否相等，有两种情况：

i==k，交换 i 和 k 的信后，它们的信和信封在正确的位置，但是其余 i-2 封信有 dp[i-2] 种错误装信的方式。由于 j 有 i-1 种取值，因此共有 (i-1)*dp[i-2] 种错误装信方式。
i != k，交换 i 和 j 的信后，第 i 个信和信封在正确的位置，其余 i-1 封信有 dp[i-1] 种错误装信方式。由于 j 有 i-1种取值，因此共有 (i-1)*dp[i-1] 种错误装信方式。

综上所述，错误装信数量方式数量为：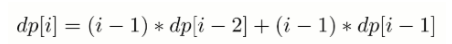
在这里插入图片描述

public int errorNum(int n) {
        if (n == 0) {
            return 0;
        }
        int[] f = new int[n + 1];
        f[0] = 0;
        f[1] = 0;
        f[2] = 1;
        for (int i = 3; i <= n; i++) {
            f[i] = (i - 1) * f[i - 2] + (i - 1) * f[i - 1];
        }
        return f[n];
    }