动态规划问题--斐波那契数列

﹏ヽ暗。殇╰゛Y 2023-01-19 14:56 272阅读 0赞

动态规划问题—斐波那契数列

1 斐波那契数列

斐波那契数列其表达式如下：

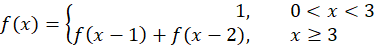
20210510233712765.png

2 递归算法

通过公式我们不难看出，其第一项和第二项为1，当x>=3时，斐波那契数列的第x项就等于其前两项的和。所以我们可以得出代码如下：







public static Integer fib(int n){
    if (n==1 || n==2){
        return 1;
    }

    return fib(n-2)+fib(n-1);
}

递归算法是自上而下的算法，要得出后面的值就得知道前两项的值，这样会产生大量重复计算，比如要求第七项的值，就需要知道第六项和第五项的值，要求第六项的值，就需要第五项和第四项的值，光这里就求了两次第五项的值，所以这种算法的效率不是很高。

3 动态规划算法

在使用递归时，我们看到了递归的不足，因为其存在大量重复函数的调用，效率很低。我们可以试试动态规划，通过保存前两项的值来求解第x项的值。其代码如下：







  1. public static Integer dp(int n){

        int[] dp = new int[n+1];

        dp[1] = 1;

        dp[2] = 1;

        for (int i = 3; i <= n; i++) {

            dp[i] = dp[i-1] + dp[i-2];

        }



        return dp[n];

    }

这里我们通过牺牲内存来保存每一项的值，就不需要重复计算而达到提高效率。到这里我们已然发现动态规划的简单原理：问题的最优解可以通过其子问题的最优解得到。若子问题有比较多的重复，则可以采用自底向上来计算。

刘玉江

2020年11月22日

发表评论

表情：
评论列表 （有 0 条评论，272人围观）

还没有评论，来说两句吧...

相关阅读

    相关 斐波那契数列问题

    问题 斐波那契数列即：1、1、2、3、5、8、13…其规律为从第三个数开始，每个数都等于它前两个数的和。那么该如何实现这一规律呢？ 方法 (1) 定义三个变量，用

    左手的ㄟ右手左手的ㄟ右手/ 0 赞/ 177 阅读