哈弗曼树的带权路径长度-蒲公英云

哈弗曼树的带权路径长度

悠悠 2023-07-17 06:08 126阅读 0赞

最近刷题刷到了这一题，此题是北邮往年复试题，看了一些网上的讲解，大多数是方法比较复杂，有些巧妙的方法又往往却缺少解释，为了方便大家理解，给小伙伴们梳理梳理

题目描述：

哈夫曼树，第一行输入一个数n，表示叶结点的个数。需要用这些叶结点生成哈夫曼树，根据哈夫曼树的概念，这些结点有权值，即weight，题目需要输出所有结点的值与权值的乘积之和。

输入描述:

输入有多组数据。
每组第一行输入一个数n，接着输入n个叶节点（叶节点权值不超过100，2<=n<=1000）。

输出描述:

输出权值。

示例

输入：
5
1 2 2 5 9

输出：
37

解题分析：

哈夫曼树的构造方法相信大家肯定都是耳熟能详的。

根据哈弗曼树构造方法，我们不妨以 {1，2，2，5，9} 节点权值举例，根据上述方法我们可以构造出其哈夫曼树为如下：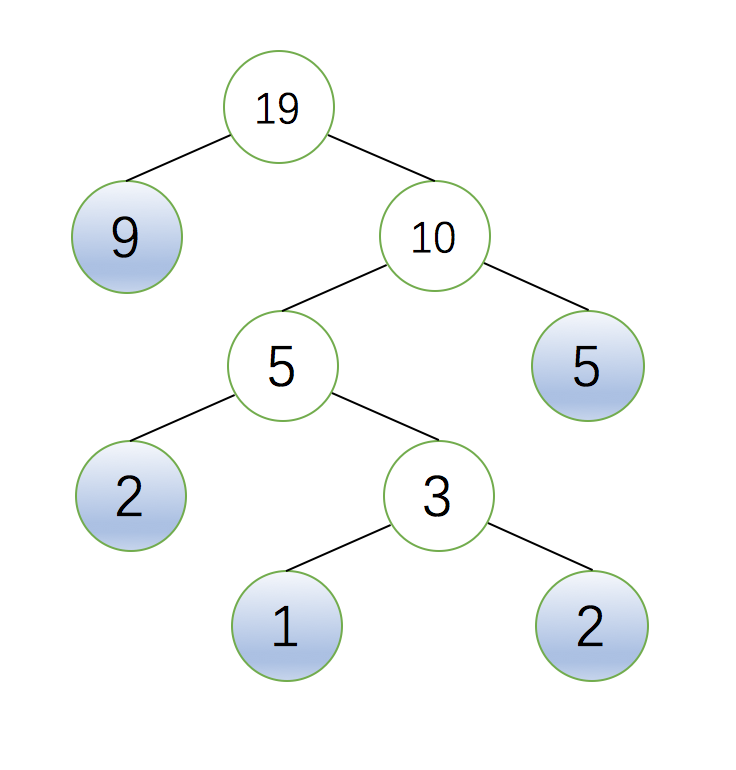
Alt
由图我们可以很容易得到带权路径长度=
37 = 9 ∗ 1 + 5 ∗ 2 + 2 ∗ 3 + 2 ∗ 4 + 1 ∗ 4 （常规） 37=9*1+5*2+2*3+2*4+1*4（常规） 37=9∗1+5∗2+2∗3+2∗4+1∗4（常规）
这是我们在建立完树后的常见计算方法，但这种方法在计算机中可不方便直接得出，我们不妨看下面一个计算式子：
1 + 2 = 3 ，2 + 3 = 5，5 + 5 = 10， 10 + 9 = 19
我们发现
3 + 5 + 10 + 19 = 37 3+5+10+19 = 37 3+5+10+19=37
有点意思，巧合吗？不，不是，你不妨思考思考3、5、10、19这些数是怎么来的……没错，它们就是由节点权值而来。
我来替你分析分析，首先按照常规方法：9x1，而19 = 10 + 9，还剩下个10；再看常规中的5，它是5x2，而剩下的10中它又可以拆分为 5 + 5，（注意，这里的一个5是来自叶节点，另一个是来自非叶节点）而来自非叶节点的5 = 2 + 3；同样，2来自叶节点，3来自非叶节点；3 = 1 + 2，这下1和2都是来自叶节点。好了，这下19我们就已经分解完了，勤奋的你在草稿纸上比划比划，你有没有发现什么？

什么！没有？
你品，你细品，你细细品……

其实你把19，10，5，3都分解完后你会发现它们其实就是叶节点的加权和，你在求它们的时候其实就已经把我们常规方法中所考虑的深度因素带进去了。

那么，计算机用这种方法来求带权路径长度会不会简单呢？没错，非常简单，这里我们再考虑用priority_queue优先队列的数据结构，就更简单啦。如果不了解这种数据结构的话，推荐可以去查查STL库，你可以把他理解为一个有序(升或降)的容器（好用的工具我们一定要学会利用）

下面我给大家贴下我的代码，仅供参考。也希望大家能在理解了上面所描述的思想后再看

//哈弗曼树
#include <stdio.h>
#include <queue>
using namespace std;
// 哈弗曼树
int main(){ 
    priority_queue<int ,vector<int>, greater<int> > p;  // 这里规定是从小到大的优先队列，默认是从大到小
    // 默认形式：priority_queue<int> p;
    int n;
    while(scanf("%d",&n) != EOF){ 
        while(!p.empty())  // 清空队列
            p.pop();
        int val;
        for(int i=0;i<n;i++){ 
            scanf("%d",&val);
            p.push(val);
        }
        int sum = 0;  // 计算带权路径长度
        while(p.size() != 1){ 
            int a = p.top(); // 取出最小的数
            p.pop();
            int b = p.top(); // 取出次小的数
            p.pop();
            sum += a+b;
            p.push(a+b);
        }
        printf("%d\n",sum);
    }
    return 0;
}