哈夫曼编码计算带权路径长度问题
哈夫曼树，又称最优二叉树，是一类带权路径长度最短的树。
也就是根节点到节点的中的长度最小，当然条件就是，每条路径都是有权重的，
所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的 路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的带权路径长度记为WPL= (W1*L1+W2*L2+W3*L3+…+Wn*Ln)
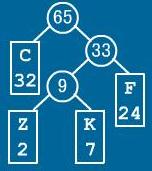
此时WPL=32×1+24×2+2×3+7×3
相关阅读
相关 哈夫曼编码计算带权路径长度问题
哈夫曼树，又称最优二叉树，是一类带权路径长度最短的树。 也就是根节点到节点的中的长度最小，当然条件就是，每条路径都是有权重的， 所谓树的带权路径长度，就是树中所有的叶结
太过爱你忘了你带给我的痛相关 Huffman Tree哈夫曼树权值路径长度WPL计算，binarytree ，Python
Huffman Tree哈夫曼树（霍夫曼树、赫夫曼树）权值路径长度WPL计算，binarytree ，Python 计算定义：把构建成功的哈夫曼树的每一个边缘节点（叶子）值乘
红太狼相关 哈弗曼树的带权路径长度
最近刷题刷到了这一题，此题是北邮往年复试题，看了一些网上的讲解，大多数是方法比较复杂，有些巧妙的方法又往往却缺少解释，为了方便大家理解，给小伙伴们梳理梳理 题目描述：
悠悠相关 数据结构--哈夫曼树-创建，带权路径长度
数据结构–哈夫曼树-创建，带权路径长度 > Project:哈夫曼树 构造 编码 译码 计算wpl > Date: 2020/02/04 > Author: WX
相关 【哈夫曼树】带权路径长度WPL
题目描述 哈夫曼树，第一行输入一个数n，表示叶结点的个数。需要用这些叶结点生成哈夫曼树，根据哈夫曼树的概念，这些结点有权值，即weight，题目需要输出所有结点的值与
相关 自动计算哈夫曼树的带权路径长度
C语言自动计算哈夫曼树的带权路径长度： include<stdio.h> include<stdlib.h> int cmp(const void a
小灰灰相关 哈夫曼树、哈夫曼编码详解
哈夫曼树介绍 hello，大家好，我是bigsai。本以为哈夫曼树、哈夫曼编码很难，结果很容易嘛！ 哈夫曼树、哈夫曼编码很多人可能听过，但是可能并没有认真学习了解，今天
╰+哭是因爲堅強的太久メ相关 哈夫曼树与哈夫曼编码
在一般的数据结构的书中，树的那章后面，著者一般都会介绍一下哈夫曼(HUFFMAN) 树和哈夫曼编码。哈夫曼编码是哈夫曼树的一个应用。哈夫曼编码应用广泛，如 JPEG中就应用
相关 哈夫曼树和哈夫曼编码
哈夫曼树 给定n个权值作为n的叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径
相关 快速求解霍夫曼编码树的带权路径长度
一、简介 霍夫曼编码被广泛的用在文本压缩编码中，但在求解霍夫曼树的WPL长度时其实不必真的构造出一棵霍夫曼树再去实际求解，在实际oj和测试时时间也不允许，求解WPL可以基
还没有评论，来说两句吧...