HZAU Little Red Riding Hood【动态规划】-蒲公英云

HZAU Little Red Riding Hood【动态规划】

傷城~ 2022-05-27 10:57 73阅读 0赞

Little Red Riding Hood

题目描述

Once upon a time, there was a little girl. Her name was Little Red Riding Hood. One day, her grandma was ill. Little Red Riding Hood went to visit her. On the way, she met a big wolf. “That’s a good idea.”，the big wolf thought. And he said to the Little Red Riding Hood, “Little Red Riding Hood, the flowers are so beautiful. Why not pick some to your grandma?” “Why didn’t I think of that? Thank you.” Little Red Riding Hood said.

Then Little Red Riding Hood went to the grove to pick flowers. There were n flowers, each flower had a beauty degree a[i]. These flowers arrayed one by one in a row. The magic was that after Little Red Riding Hood pick a flower, the flowers which were exactly or less than d distances to it are quickly wither and fall, in other words, the beauty degrees of those flowers changed to zero. Little Red Riding Hood was very smart, and soon she took the most beautiful flowers to her grandma’s house, although she didn’t know the big wolf was waiting for her. Do you know the sum of beauty degrees of those flowers which Little Red Riding Hood pick?

输入

The first line input a positive integer T (1≤T≤100), indicates the number of test cases. Next, each test case occupies two lines. The first line of them input two positive integer n and

k (2 <= n <= 10^5 ) ,1 <= k <= n ), the second line of them input n positive integers a (1<=a <=10^5)

输出

Each group of outputs occupies one line and there are one number indicates the sum of the largest beauty degrees of flowers Little Red Riding Hood can pick.

样例输入

1
3 1
2 1 3

样例输出

5

题目概括：

有n朵花在一排上，每朵花都有一个权值，每摘下一朵花，其在k距离内的话都会凋谢，其权值也变为零。求能得到的最大权值之和。

解题分析：

这道题是一个动态规划，对于每一朵花都要算出其前边距离大于k的权值的最大和。

动态转移方程：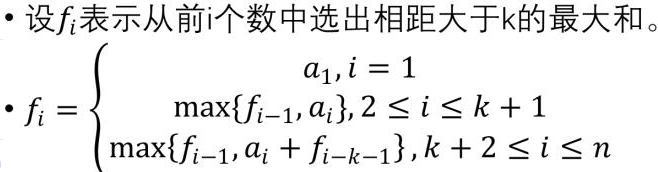
这里写图片描述

测试数据：

2
5 2
2 1 3 4 7
6 2
2 1 1 3 4 7

测试数据输出：

9
9

AC代码：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define N 100005
int a[N];
int main()
{
    int i, j, k, n, T;
    scanf("%d", &T);
    while(T--){
        scanf("%d%d", &n, &k);
        for(i = 1; i <= n; i++) scanf("%d", &a[i]);
        for(i = 2; i <= k+1; i++) a[i] = max(a[i], a[i-1]);
        for(i = k+2; i <= n; i++){
            a[i] = max(a[i-k-1]+a[i], a[i-1]);
        }
        printf("%d\n", a[n]);
    }
    return 0;
}