铺瓷砖

雨点打透心脏的1/2处 2023-02-16 06:17 30阅读 0赞

## 一、前言 ##

问题来源LeetCode 1240，难度：困难

问题链接：[https://leetcode-cn.com/problems/tiling-a-rectangle-with-the-fewest-squares][https_leetcode-cn.com_problems_tiling-a-rectangle-with-the-fewest-squares]

## 二、题目 ##

你是一位施工队的工长，根据设计师的要求准备为一套设计风格独特的房子进行室内装修。

房子的客厅大小为 n x m，为保持极简的风格，需要使用尽可能少的 正方形 瓷砖来铺盖地面。假设正方形瓷砖的规格不限，边长都是整数。请你帮设计师计算一下，最少需要用到多少块方形瓷砖？

示例 1：

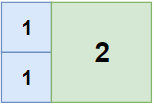
![20200608203058847.png][]

输入：n = 2, m = 3
    输出：3
    解释：3 块地砖就可以铺满卧室。
         2 块 1x1 地砖
         1 块 2x2 地砖

示例 2

![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE_size_16_color_FFFFFF_t_70][]

示例 3：

![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE_size_16_color_FFFFFF_t_70 1][]

输入：n = 11, m = 13
    输出：6

提示：

1 <= n <= 13

1 <= m <= 13

## 三、思路 ##

### 3.1 整体切割 ###

我们先来看这种情况，当矩形（长m，宽n），如果m 远大于n（m大于n两倍以上），我们可以直接将其逐渐切割下一个 nxn 的矩形，此时剩下的 长如果还是n两倍以上继续切割，切割到什么时候为止呢，m >= n+1 && m <= 2n-1。 贪心算法思路。

![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE_size_16_color_FFFFFF_t_70 2][]

### 3.2 精细切割 ###

经过整体切割之后，剩下的矩形（长n，宽m），m >= n+1 && m <= 2n-1。可以用三种切割方法

**1.横切**

![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE_size_16_color_FFFFFF_t_70 3][]

**2. 竖切**

![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE_size_16_color_FFFFFF_t_70 4][]

### 3. 组合切割，中间会有一个1X1的正方形。 ###

![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE_size_16_color_FFFFFF_t_70 5][]

前两种好理解，最难理解的是最后一种情况，最后一种情况我们可以用暴力法确定这个正方形可能在任意一个指标上。这里提供一种方法最优确定这个正方形方法。如上图 n = 2L + 1, m = 2L + 3，即：m = n + 2 (n >= 5 && n为偶数)。为什么这种长宽下的矩形中，包含一个1X1的矩形可能是最小切割呢？我也证明不出来，只是在画图并用贪心得最大正方形的时候经过公式推导出来的这个公式。在leetcode中验证是可以通过，执行速度很快。

![20200608203514226.png][]

### 3.3 解决方案 ###

提供用5个解决方法，后面两种是leetcode中别人的解决方法。

方法一：动态规划—自顶向下，不带备忘录

方法二：动态规划—自顶向下，带备忘录。（先做了一次贪心算法，在宽较小，长很大的时候效率更好）

方法三：动态规划—自低向上

方法四：动态规划—自低向上，网上解题方法，用于验证

方法五：动态规划—自低向上，网上解题方法，用于验证

需要说明：leetcode中测试用例并不够全面，在测试过程中发现自己写的一种解决方案通过了测试，但是在本地测试增加测试用例的时候结果和方式四、方法输出结果不一样。

## 四、编码实现 ##

//==========================================================================
    /**
    * @file : 1240_TilingRectangle.h
    * @title: 铺瓷砖
    * @purpose : 你是一位施工队的工长，根据设计师的要求准备为一套设计风格独特的房子进行室内装修。
    * 房子的客厅大小为 n x m，为保持极简的风格，需要使用尽可能少的 正方形 瓷砖来铺盖地面。
    * 假设正方形瓷砖的规格不限，边长都是整数。
    * 请你帮设计师计算一下，最少需要用到多少块方形瓷砖？
    *
    * 来源：力扣（LeetCode）难道：困难
    * 链接：https://leetcode-cn.com/problems/tiling-a-rectangle-with-the-fewest-squares
    * 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
    */
    //==========================================================================
    
    #include <vector>
    #include <iostream>
    #include <algorithm>
    using namespace std;
    
    #define NAMESPACE_TILINGRECTANGLE namespace NAME_TILINGRECTANGLE {
    #define NAMESPACE_TILINGRECTANGLEEND }
    NAMESPACE_TILINGRECTANGLE
    
    // 动态规划—自顶向下
    // 不带备忘录
    class Solution_1
    {
    public:
    	int tilingRectangle(int n, int m)
    	{
    		if (n == 0 || m == 0)
    			return 0;
    
    		int minn = min(n, m);
    		int maxn = max(n, m);
    
    		int r = maxn / minn;
    		int mod = maxn % minn;
    		if (mod == 0)
    			return r;
    
    		int add = 0;
    		if (r >= 2)
    		{
    			add = r - 1;
    			maxn = minn + mod;
    		}
    
    		int ret = 0x7FFFFFFF;
    		// 横切
    		for (int i = 1; i <= minn / 2; ++i)
    			ret = min(ret, tilingRectangle(maxn, i) + tilingRectangle(maxn, minn - i));
    		
    
    		// 竖切
    		for (int i = 1; i <= maxn / 2; ++i)
    			ret = min(ret, tilingRectangle(minn, i) + tilingRectangle(minn, maxn - i));
    		
    
    		// 中间有个1X1的正方形
    		if (minn >= 5 && minn % 2 == 1 && minn + 2 == maxn)
    			ret = min(ret, 4 + tilingRectangle(minn / 2 - 1, minn / 2 + 3));
    
    		return ret + add;
    	}
    };
    
    // 动态规划—自顶向下
    // 带备忘录
    class Solution_2
    {
    public:
    	int tilingRectangle(int n, int m)
    	{
    		vector<vector<int>> dp(1000, vector<int>(1000, 0));
    		return tilingRectangle(n, m, dp);
    	}
    
    	int tilingRectangle(int n, int m, vector<vector<int>>& dp)
    	{
    		int minn = min(n, m);
    		int maxn = max(n, m);
    
    		if (dp[minn][maxn] != 0)
    		{
    			return dp[minn][maxn];
    		}
    
    		if (n == 0 || m == 0)
    			return 0;
    
    		int r = maxn / minn;
    		int mod = maxn % minn;
    		if (mod == 0)
    		{
    			dp[minn][maxn] = r;
    			return r;
    		}
    		int add = 0;
    		if (r >= 2)
    		{
    			add = r - 1;
    			maxn = minn + mod;
    		}
    
    		int ret = 0x7FFFFFFF;
    
    		// 横切
    		for (int i = 1; i <= minn / 2; ++i)
    			ret = min(ret, tilingRectangle(maxn, i, dp) + tilingRectangle(maxn, minn - i, dp));
    
    		// 竖切
    		for (int i = 1; i <= maxn / 2; ++i)
    			ret = min(ret, tilingRectangle(minn, i, dp) + tilingRectangle(minn, maxn - i, dp));
    
    		// 中间有个1X1的正方形
    		if (minn >= 5 && minn % 2 == 1 && minn + 2 == maxn)
    			ret = min(ret, 4 + tilingRectangle(minn / 2 - 1, minn / 2 + 3, dp));
    
    		dp[min(n, m)][max(n, m)] = ret + add;
    		return ret + add;
    	}
    };
    
    // 动态规划—自低向上
    class Solution_3
    {
    public:
    	int tilingRectangle(int n, int m)
    	{
    		vector<vector<int>> dp(n+1, vector<int>(m+1, 0));
    		for (int i = 1; i <= n; ++i)
    		{
    			for (int j = 1; j <= m; ++j)
    			{
    				dp[i][j] = INT_MAX;
    				if (i == j)
    				{
    					dp[i][j] = 1;
    					continue;
    				}
    
    				for (int r = 1; r <= i / 2; ++r)
    					dp[i][j] = min(dp[i][j], dp[r][j] + dp[i - r][j]);
    
    				for (int c = 1; c <= j / 2; ++c)
    					dp[i][j] = min(dp[i][j], dp[i][c] + dp[i][j - c]);
    
    				// 中间有个1X1的正方形 
    				int minn = min(i, j);
    				int maxn = max(i, j);
    				if (minn >= 5 && minn % 2 == 1 && minn + 2 == maxn)
    					dp[i][j] = min(dp[i][j], 4 + dp[minn / 2 - 1][minn / 2 + 3]);
    			}
    		}
    
    		return dp[n][m];
    	}
    };
    
    // 网上解题方法
    // 动态规划—自低向上
    class Solution_4
    {
    public:
        int tilingRectangle(int n, int m)
        {
            if (max(n, m) == 13 && min(n, m) == 11) return 6;
            vector<vector<int>> dp(n + 1, vector<int>(m + 1));
            for (int i = 1; i <= n; ++i)
                for (int j = 1; j <= m; ++j)
                {
                    dp[i][j] = INT_MAX;
                    if (i == j)
                    {
                        dp[i][j] = 1;
                        continue;
                    }
                    for (int r = 1; r <= i / 2; ++r)
                        dp[i][j] = min(dp[i][j], dp[r][j] + dp[i - r][j]);
                    for (int c = 1; c <= j / 2; ++c)
                        dp[i][j] = min(dp[i][j], dp[i][c] + dp[i][j - c]);
                }
            return dp[n][m];
        }
    };
    
    // 网上解题方法
    // 动态规划—自低向上
    class Solution_5 
    {
    public:
    	int tilingRectangle(int n, int m) 
    	{
    		vector<vector<int>> dp(n+1, vector<int>(m+1,0));
    		for (int i = 1; i <= n; i++)
    		{
    			for (int j = 1; j <= m; j++)
    			{
    				dp[i][j] = INT_MAX;
    				if (i == j) 
    				{
    					dp[i][j] = 1;
    					continue;
    				}
    				// 横切
    				for (int r = 1; r <= i / 2; r++) 
    					dp[i][j] = min(dp[i][j], dp[r][j] + dp[i - r][j]);
    
    				// 竖切
    				for (int c = 1; c <= j / 2; c++) 
    					dp[i][j] = min(dp[i][j], dp[i][c] + dp[i][j - c]);
    				
    				// 中心一个单元格
    				for (int p = 1; p <= i; p++)
    				{
    					for (int q = 1; q <= j; q++) 
    					{
    						dp[i][j] = min(dp[i][j], 1 + dp[p - 1][q] + dp[i - p + 1][q - 1] + dp[i - p][j - q + 1] + dp[p][j - q]);
    					}
    				}
    					
    			}
    		}
    
    		return dp[n][m];
    	}
    };
    
    //
    // 测试 用例 START
    void test(const char* testName, int n, int m, int expect)
    {
    	//Solution_1 S1;
    	Solution_2 S2;
    	Solution_3 S3;
    	Solution_4 S4;
    	Solution_5 S5;
    
    	int result2 = S2.tilingRectangle(n, m);
        int result3 = S3.tilingRectangle(n, m);
    	int result4 = S4.tilingRectangle(n, m);
    	int result5 = S5.tilingRectangle(n, m);
    
        // 粗略验证一下
    	if (result2 == result3 && result2 == result4 && result2 == result5)
    	{
    		cout << testName << ", solution passed." << endl;
    	}
    	else
    	{
    		cout << testName << ", solution failed. result2:" << result2 << ", result3:" << result3 << ", result4:" << result4 << ", result5:" << result5 << endl;
    	}
    }
    
    // 测试用例
    void Test1()
    {
        int n = 1;
        int m = 1;
        int expect = 1;
    
        test("Test1()", n, m, expect);
    }
    
    void Test2()
    {
        int n = 1;
        int m = 2;
        int expect = 2;
    
        test("Test2()", n, m, expect);
    }
    
    void Test3()
    {
        int n = 2;
        int m = 3;
        int expect = 3;
    
        test("Test3()", n, m, expect);
    }
    
    void Test4()
    {
        int n = 13;
        int m = 11;
        int expect = 6;
    
        test("Test4()", n, m, expect);
    }
    
    void Test5()
    {
        int n = 4;
        int m = 6;
        int expect = 3;
    
        test("Test5()", n, m, expect);
    }
    
    void Test6()
    {
        int n = 7;
        int m = 6;
        int expect = 5;
    
        test("Test6()", n, m, expect);
    }
    
    void Test7()
    {
        int n = 5;
        int m = 8;
        int expect = 5;
    
        test("Test7()", n, m, expect);
    }
    
    void Test8()
    {
        int n = 10;
        int m = 9;
        int expect = 6;
    
        test("Test8()", n, m, expect);
    }
    
    void Test9()
    {
    	int n = 7;
    	int m = 4;
    	int expect = 5;
    
    	test("Test9()", n, m, expect);
    }
    
    void Test10()
    {
    	int n = 12;
    	int m = 11;
    	int expect = 7;
    
    	test("Test10()", n, m, expect);
    }
    
    void Test11()
    {
    	int n = 9;
    	int m = 7;
    	int expect = 6;
    
    	test("Test11()", n, m, expect);
    }
    
    void Test12()
    {
    	int n = 22;
    	int m = 25;
    	int expect = 0;
    
    	test("Test12()", n, m, expect);
    }
    
    void Test13()
    {
    	int n = 30;
    	int m = 37;
    	int expect = 7;
    
    	test("Test13()", n, m, expect);
    }
    
    void Test14()
    {
    	int n = 15;
    	int m = 16;
    	int expect = 0;
    
    	test("Test14()", n, m, expect);
    }
    
    void Test15()
    {
    	int n = 100;
    	int m = 99;
    	int expect = 0;
    
    	test("Test15()", n, m, expect);
    }
    
    void Test16()
    {
    	int n = 200;
    	int m = 3;
    	int expect = 0;
    
    	test("Test16()", n, m, expect);
    }
    
    void Test17()
    {
    	int n = 513;
    	int m = 899;
    	int expect = 0;
    
    	test("Test17()", n, m, expect);
    }
    
    NAMESPACE_TILINGRECTANGLEEND
    // 测试 用例 END
    //
    
    void TilingRectangle_Test()
    {
        NAME_TILINGRECTANGLE::Test1();
        NAME_TILINGRECTANGLE::Test2();
        NAME_TILINGRECTANGLE::Test3();
        NAME_TILINGRECTANGLE::Test4();
        NAME_TILINGRECTANGLE::Test5();
        NAME_TILINGRECTANGLE::Test6();
        NAME_TILINGRECTANGLE::Test7();
        NAME_TILINGRECTANGLE::Test8();
        NAME_TILINGRECTANGLE::Test9();
        NAME_TILINGRECTANGLE::Test10();
        NAME_TILINGRECTANGLE::Test11();
        NAME_TILINGRECTANGLE::Test12();
        NAME_TILINGRECTANGLE::Test13();
        NAME_TILINGRECTANGLE::Test14();
        //NAME_TILINGRECTANGLE::Test15();
        //NAME_TILINGRECTANGLE::Test16();	// 测试时间较长
        //NAME_TILINGRECTANGLE::Test17();	// 测试时间较长
    }

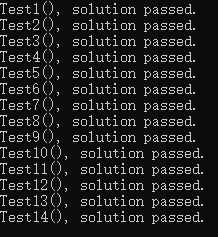
**执行结果：**

![20200608203639917.png][]

[https_leetcode-cn.com_problems_tiling-a-rectangle-with-the-fewest-squares]: https://leetcode-cn.com/problems/tiling-a-rectangle-with-the-fewest-squares
[20200608203058847.png]: https://img-blog.csdnimg.cn/20200608203058847.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE_size_16_color_FFFFFF_t_70]: https://img-blog.csdnimg.cn/20200608203129411.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE=,size_16,color_FFFFFF,t_70
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE_size_16_color_FFFFFF_t_70 1]: https://img-blog.csdnimg.cn/20200608203152931.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE=,size_16,color_FFFFFF,t_70
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE_size_16_color_FFFFFF_t_70 2]: https://img-blog.csdnimg.cn/20200608203320748.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE=,size_16,color_FFFFFF,t_70
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE_size_16_color_FFFFFF_t_70 3]: https://img-blog.csdnimg.cn/20200608203347614.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE=,size_16,color_FFFFFF,t_70
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE_size_16_color_FFFFFF_t_70 4]: https://img-blog.csdnimg.cn/20200608203420764.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE=,size_16,color_FFFFFF,t_70
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE_size_16_color_FFFFFF_t_70 5]: https://img-blog.csdnimg.cn/20200608203449419.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L25pZTIzMTQ1NTA0NDE=,size_16,color_FFFFFF,t_70
[20200608203514226.png]: https://img-blog.csdnimg.cn/20200608203514226.png
[20200608203639917.png]: https://img-blog.csdnimg.cn/20200608203639917.png