图的最短路径之Floyd算法C/C++代码实现-蒲公英云

图的最短路径之Floyd算法C/C++代码实现

弗洛伊德Floyd算法：

也称插点法，该算法用来求解每一对顶点之间的最短路径

假设从顶点1到2，顶点3为过度中间顶点则：
如果某个顶点位于从起点到终点的最短路径上：
1->2=（1->3）+（3->2）
如果某个顶点不在从起点到终点的最短路径上：
1->2<（1->3）+（3->2）

总结：从i号顶点到j号顶点只经过前k号点的最短路径
以该图为例：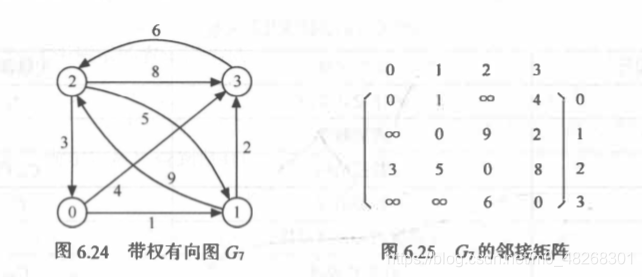
在这里插入图片描述

辅助数组的变化过程：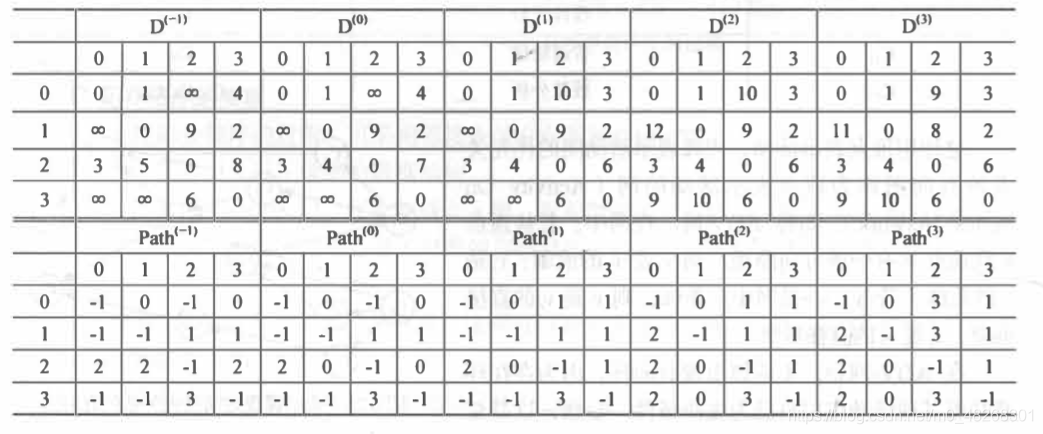
在这里插入图片描述

代码如下：

#include<stdio.h>
#define MaxInt 999            //定义无穷大
#define MVNum 100
typedef char VerTexType;    //顶点类型
typedef int ArcType;        //边权值类型
//邻接矩阵存储结构
typedef struct
{
    VerTexType vexs[MVNum];                //顶点表
    ArcType arcs[MVNum][MVNum];            //邻接矩阵
    int vexnum, arcnum;                    //图的当前点数和边数
}AMGraph;
void printGraph(AMGraph G);
int LocateVex(AMGraph G, char v);
//创建有向网
void CreateUDN(AMGraph &G)
{
    G.vexnum = 4;                        //输入总顶点数和边数
    G.arcnum = 8;
    G.vexs[0] = 'v0';                    //输入顶点信息
    G.vexs[1] = 'v1';
    G.vexs[2] = 'v2';
    G.vexs[3] = 'v3';
    for (int i = 0; i < G.vexnum; i++)            //初始化邻接矩阵为极大值
    {
        for (int j = 0; j < G.vexnum; j++)
        {
            G.arcs[i][j] = MaxInt;
        }
    }
    //输入权值
    int i, j;
    i = LocateVex(G, 'v0');
    j = LocateVex(G, 'v1');
    G.arcs[i][j] = 1;
    i = LocateVex(G, 'v0');
    j = LocateVex(G, 'v3');
    G.arcs[i][j] = 4;
    i = LocateVex(G, 'v1');
    j = LocateVex(G, 'v3');
    G.arcs[i][j] = 2;
    i = LocateVex(G, 'v1');
    j = LocateVex(G, 'v2');
    G.arcs[i][j] = 9;
    i = LocateVex(G, 'v2');
    j = LocateVex(G, 'v0');
    G.arcs[i][j] = 3;
    i = LocateVex(G, 'v2');
    j = LocateVex(G, 'v1');
    G.arcs[i][j] = 5;
    i = LocateVex(G, 'v2');
    j = LocateVex(G, 'v3');
    G.arcs[i][j] = 8;
    i = LocateVex(G, 'v3');
    j = LocateVex(G, 'v2');
    G.arcs[i][j] = 6;
    //自己到自己初始化为0
    i = LocateVex(G, 'v0');
    j = LocateVex(G, 'v0');
    G.arcs[i][j] = 0;
    i = LocateVex(G, 'v1');
    j = LocateVex(G, 'v1');
    G.arcs[i][j] = 0;
    i = LocateVex(G, 'v2');
    j = LocateVex(G, 'v2');
    G.arcs[i][j] = 0;
    i = LocateVex(G, 'v3');
    j = LocateVex(G, 'v3');
    G.arcs[i][j] = 0;
    printGraph(G);
}
//返回顶点在数组中的下标
int LocateVex(AMGraph G, char v)
{
    for (int i = 0; i < G.vexnum; i++)
    {
        if (G.vexs[i] == v)
        {
            return i;
        }
    }
}
//打印输出邻接矩阵
void printGraph(AMGraph G)
{
    for (int i = 0; i < G.vexnum; i++)
    {
        printf("v%d :", i + 1);
        for (int j = 0; j < G.vexnum; j++)
        {
            printf("%5d ", G.arcs[i][j]);
        }
        printf("\n");
    }
}
//邻接矩阵深度优先遍历
bool visited[MVNum];
void DFS_AM(AMGraph G, int v)
{
    printf("v%c->", G.vexs[v]);
    visited[v] = true;
    for (int w = 0; w < G.vexnum; w++)
    {
        if ((G.arcs[v][w]) != 0 && (!visited[w]))
        {
            DFS_AM(G, w);
        }
    }
}
//最短路径弗洛伊德算法
int D[MVNum][MVNum];            //存放v0到vi的最短路径长度值
int Path[MVNum][MVNum];            //存放vi的直接前驱顶点序号
void ShortestPath_Floyd(AMGraph G)
{
    //初始化
    for (int i = 0; i<G.vexnum; i++)
    {
        for (int j = 0; j<G.vexnum; j++)
            {
                D[i][j] = G.arcs[i][j];
                if (D[i][j] < MaxInt)        //i和j之间有弧
                {
                    Path[i][j] = i;
                }
                else 
                {
                    Path[i][j] =-1;
                }
            }
    }
    //算法开始
    for (int k = 0; k < G.vexnum; k++)            //过度顶点
    {
        for (int i = 0; i < G.vexnum; i++)        //起点
        {
            for (int j = 0; j < G.vexnum; j++)    //终点
            {
                if (D[i][k] + D[k][j] < D[i][j])        //如小于更新D[i][j]
                {
                    D[i][j] = D[i][k] + D[k][j];
                    Path[i][j] = Path[k][j];
                }
            }
        }
    }
}
//打印输出辅助数组D[i][j]和Path[i][j]
void printArray(AMGraph G)
{
    printf("\nD数组：\n");
    for (int i = 0; i < G.vexnum; i++)
    {
        printf("%d:", i);
        for (int j = 0; j < G.vexnum; j++)
        {
            printf("%5d", D[i][j]);
        }
        printf("\n");
    }
    printf("\nPath数组：\n");
    for (int i = 0; i < G.vexnum; i++)
    {
        printf("%d:", i);
        for (int j = 0; j < G.vexnum; j++)
        {
            printf("%5d", Path[i][j]);
        }
        printf("\n");
    }
}
int main()
{
    AMGraph G;
    CreateUDN(G);
    int v = 0;
    printf("深度优先遍历：：");
    DFS_AM(G, v);
    int v0 = 0;
    printf("\n====================================\n");
    ShortestPath_Floyd(G);
    printArray(G);    //输出辅助数组D和Path
}