区间DP | 2：环上的合并石子 —— 例题：合并石子（环形）

傷城~ 2023-07-17 07:28 150阅读 0赞

本文是在区间DP | 1：矩阵链乘问题（含优化） —— 例题：矩阵链乘、合并石子 上的升级（建议先看链接文章）。从链到环的改变，但本质还是区间dp问题，将环的区间任然解析成链即可。

  1. 环上的合并石子问题：环形排列着N堆石子，现在要将石子合并成一堆。规定如下：每次只能将相邻的两堆石子合并，合并两堆石子所花费的时间为两堆石子的数量和。求将N堆石子合并成一堆最小花费的时间。（石子分为n堆，石子的数量存储在数组p[0..n-1]中）

若将此题的环一条条转成线来机械的运算：考虑为 n 个线型的合并石子，时间复杂度上必将增加一个幂次，不够划算，下面有更好的方法。（其实仔细想想，n次调用线型的合并石子的模型，其实存在大量重复计算）

本文**目录**

方法一：直接刚！将数组环形考虑 —— 时间复杂度O(n^3)

方法二：化圆为直 —— 时间复杂度O(n^3)

  1.      方法三： 化圆为直优化版 —— 时间复杂度![\\bg\_white O(n^2)][bg_white O_n_2]

end

" class="reference-link">方法一：直接刚！将数组环形考虑 —— 时间复杂度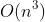O(n^3)

既然是环形的，我们将数组环形地去考虑即可，只是因为各种临界问题，代码比较复杂，要注意细节~（实在是太琐碎了！写了两个小时才把bug清理完，流下了惨痛的泪水，所以后又改进了方法，详见方法二）

相较于原方法，核心部分是三层循环，但是由于环形的两端连接问题，第2、3层循环均需要改动：

  • 第一层循环：长度 l = 2..n
  • 第二层循环：讨论每个长度为 l 的石子堆 p\_\{i..j\}：i = 1..n， j = ( i + l + 1 ) % n（此循环体内计算sum也是复杂了些，建议单独写出一个calcSum函数计算）
  • 第三层循环：确定最优分割点 k = i..j-1

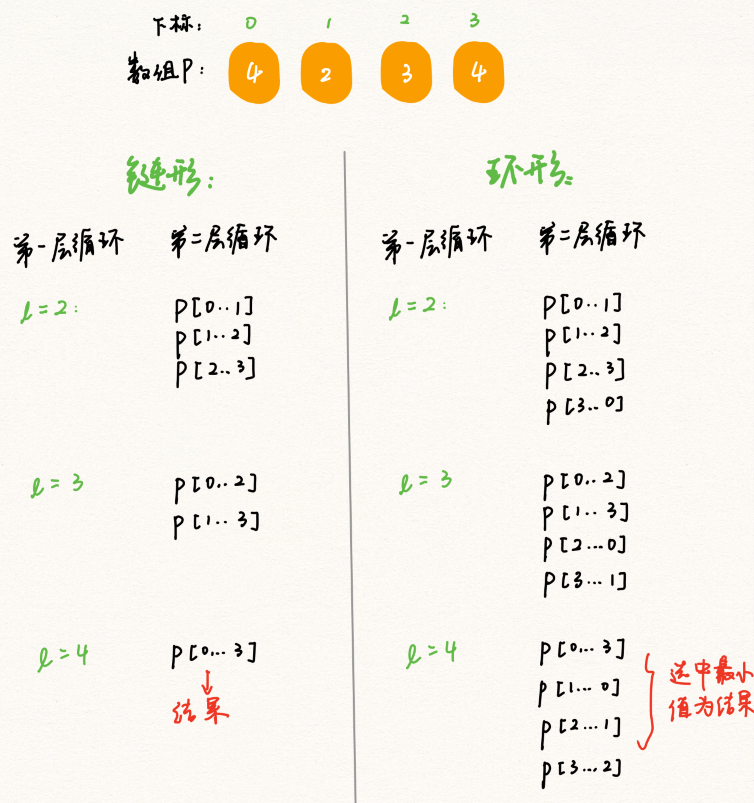
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80Mzc4NzA0Mw_size_16_color_FFFFFF_t_70

两种方法对应的ans数组的填充也是不同的：

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80Mzc4NzA0Mw_size_16_color_FFFFFF_t_70 1

代码实现：

注意临界问题！注意琐碎的临界问题！十分注意琐碎的临界问题！！！

  1. #define N 100
  3. #include <cstdio>
  4. #include <algorithm>
  5. #include <climits>
  6. using namespace std;
  8. /* 合并石子问题：环形排列着N堆石子，现在要将石子合并成一堆。
  9.  * 规定如下：每次只能将相邻的两堆石子合并，合并两堆石子所花费的时间为两堆石子的数量和。
  10.  * 求将N堆石子合并成一堆最小花费的时间。（石子分为n堆，石子的数量存储在数组p[0..n-1]中）*/
  12. int ans[N][N] = {0};
  13. int s = 0;  //所有石子堆的总和（提前计算好）
  15. /* 计算p[i..j]的石子总和 (由于是环形，j可以小于i)*/
  16. int calcSum(int p[], int l, int r, int n) {
  17.     /* 特殊考虑完整（包含了全部石堆）的情况 */
  18.     if (l - r == 1 || r - l + 1 == n)
  19.         return s;
  20.     /* 正常计算 */
  21.     int sum = 0;
  22.     for (int i = l; i != (r + 1) % n; i = (i + 1) % n)
  23.         sum += p[i];
  24.     return sum;
  25. }
  27. int MergeStone(int p[], int n) {
  29.     int min_ans = INT_MAX;
  30.     /* 石子堆的个数：从1到n */
  31.     for (int l = 2; l <= n; l++) {
  32.         /* 讨论l个石子的石子堆 p[i..j](由于是环形，j可以小于i) */
  33.         for (int i = 0; i < n; i++) {
  34.             int j = (i + l - 1) % n;
  35.             int sum = calcSum(p, i, j, n);
  36.             ans[i][j] = INT_MAX;
  37.             /* 依次讨论每一个分割点d:将石子堆p[i..j]分成p[i..k]和 A[k+1..j] */
  38.             for (int k = i; k != j; k = (k + 1) % n)
  39.                 ans[i][j] = min(ans[i][k] + ans[(k + 1) % n][j] + sum, ans[i][j]);
  40.             /* l = n 即我们需要的答案范围，找出最小值 */
  41.             if(l == n) {
  42.                 min_ans = min(ans[i][j], min_ans);
  43.             }
  44.         }
  45.     }
  46.     return min_ans;
  47. }
  49. int main() {
  50.     int n = 4;
  51.     int p[] = {4, 2, 3, 4};
  52.     for (int i = 0; i < n; i++)
  53.         s += p[i];
  54.     printf("%d\n", MergeStone(p, n));
  55. }

" class="reference-link">方法二：化圆为直 —— 时间复杂度O(n^3)

为方便遍历，可以考虑化圆为直：把圆形剪开 —— 假设石子堆为1、2、3，那么剪开的石子堆为1、2、3、1、2，那么如果原数组 p 长度为 n， 那么经过我们的剪开操作，长度变为 2n - 1。接下来就是和线型的合并石子问题一样了。

唯一的区别是：对于线型的2n - 1 个石子堆，我们的结果不是选取 L = 2n - 1的，而是 L= n 中所有结果的最小值。

代码实现：

（在未改进的线形合并石子问题上改的，故时间复杂度也为O(n^3)）

  1. #define MAX 100
  3. #include <cstdio>
  4. #include <climits>
  5. #include <algorithm>
  7. using namespace std;
  8. /* 合并石子问题：环形排列着N堆石子，现在要将石子合并成一堆。
  9.  * 规定如下：每次只能将相邻的两堆石子合并，合并两堆石子所花费的时间为两堆石子的数量和。
  10.  * 求将N堆石子合并成一堆最小花费的时间。（石子分为n堆，石子的数量存储在数组p[0..n-1]中）*/
  11. int ans[2 * MAX][2 * MAX] = {0};
  13. /* 将环形的石子化为线形 */
  14. void GetList(int p[], int n) {
  15.     int j = 0;
  16.     for (int i = n; i < 2 * n - 1; i++)
  17.         p[i] = p[j++];
  18. }
  20. int MergeStone(int p[], int n) {
  22.     GetList(p, n);  //化圆为直
  23.     int min_ans = INT_MAX;
  24.     int N = 2 * n - 1;// 线形中石子堆个数看做 2n - 1
  25.     /* 石子堆的个数：从1到n */
  26.     for (int l = 2; l <= n; l++) {
  27.         /* 讨论l个石子的石子堆 p[i..j] */
  28.         for (int i = 0; i < N - l + 1; i++) {
  29.             int j = i + l - 1;
  30.             /* 计算石子堆p[i..j]的总数 */
  31.             int sum = 0;
  32.             for (int t = i; t <= j; t++)
  33.                 sum += p[t];
  35.             /* 依次讨论每一个分割点d:将石子堆p[i..j]分成p[i..k]和 A[k+1..j] */
  36.             ans[i][j] = INT_MAX;
  37.             for (int k = i; k < j; k++)
  38.                 ans[i][j] = min(ans[i][k] + ans[k + 1][j] + sum, ans[i][j]);
  39.             /* l = n 即我们需要的答案范围，找出最小值 */
  40.             if (l == n) {
  41.                 min_ans = min(ans[i][j], min_ans);
  42.             }
  43.         }
  44.     }
  45.     return min_ans;
  46. }

" class="reference-link">方法三： 化圆为直优化版 —— 时间复杂度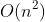\\bg\_white O(n^2)

同区间DP | 1：矩阵链乘问题（含优化） —— 例题：矩阵链乘、合并石子中的改进方法，新增最优决策点，存储于divide数组中。

代码实现：

  1. #define MAX 100
  3. #include <cstdio>
  4. #include <climits>
  5. #include <algorithm>
  7. using namespace std;
  8. /* 合并石子问题：环形排列着N堆石子，现在要将石子合并成一堆。
  9.  * 规定如下：每次只能将相邻的两堆石子合并，合并两堆石子所花费的时间为两堆石子的数量和。
  10.  * 求将N堆石子合并成一堆最小花费的时间。（石子分为n堆，石子的数量存储在数组p[0..n-1]中）*/
  12. // 改进版2！！！！！
  13. int ans[2 * MAX][2 * MAX] = {0};
  14. int divide[2 * MAX][2 * MAX] = {0};
  16. /* 将环形的石子化为线形 */
  17. void GetList(int p[], int n) {
  18.     int j = 0;
  19.     for (int i = n; i < 2 * n - 1; i++)
  20.         p[i] = p[j++];
  21. }
  23. void initDivideArray(int n) {
  24.     for (int i = 0; i < n; i++)
  25.         divide[i][i] = i;
  26. }
  28. int MergeStone(int p[], int n) {
  30.     GetList(p, n);  //化圆为直
  31.     int min_ans = INT_MAX;
  32.     int N = 2 * n - 1;// 线形中石子堆个数看做 2n - 1
  33.     initDivideArray(N);  //初始化divide数组
  35.     /* 石子堆的个数：从1到n */
  36.     for (int l = 2; l <= n; l++) {
  37.         /* 讨论l个石子的石子堆 p[i..j] */
  38.         for (int i = 0; i < N - l + 1; i++) {
  39.             int j = i + l - 1;
  40.             /* 计算石子堆p[i..j]的总数 */
  41.             int sum = 0;
  42.             for (int t = i; t <= j; t++)
  43.                 sum += p[t];
  45.             /* 依次讨论每一个分割点d:将石子堆p[i..j]分成p[i..k]和 A[k+1..j] */
  46.             ans[i][j] = INT_MAX;
  47.             for (int temp, k = divide[i][j - 1]; k <= divide[i + 1][j]; k++) {
  48.                 temp = ans[i][k] + ans[k + 1][j] + sum;
  49.                 if (temp < ans[i][j]) {
  50.                     ans[i][j] = temp;
  51.                     divide[i][j] = k;
  52.                 }
  53.             }
  55.             /* l = n 即我们需要的答案范围，找出最小值 */
  56.             if (l == n) {
  57.                 min_ans = min(ans[i][j], min_ans);
  58.             }
  59.         }
  60.     }
  61.     return min_ans;
  62. }

增加一点点难度 —— 同时求最大最小

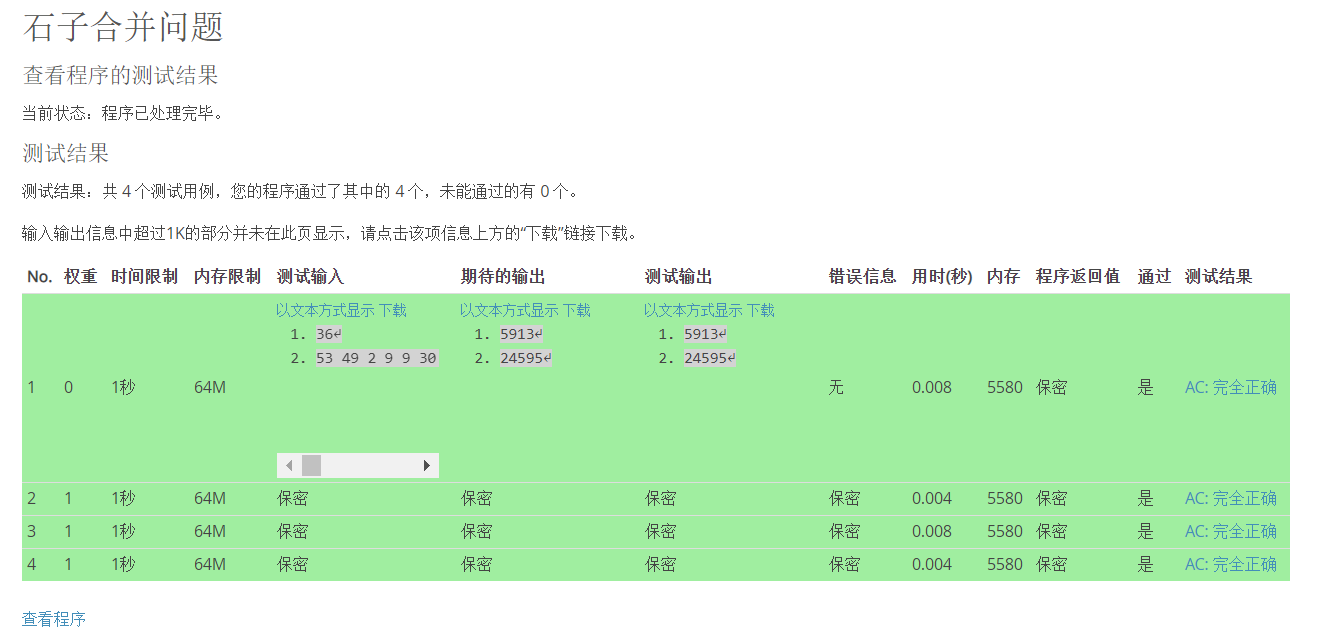
石子合并问题






















成绩 10 开启时间 2020年03月24日 星期二 23:15
折扣 0.8 折扣时间 2020年04月21日 星期二 23:55
允许迟交 否 关闭时间 2020年04月21日 星期二 23:55

问题描述: 在一个圆形操场的四周摆放着n堆石子. 现在要将石子有次序地合并成一堆. 规定每次只能选相邻的2堆石子合并成一堆, 并将新的一堆石子数记为该次合并的得分. 试设计一个算法, 计算出将n堆石子合并成一堆的最小得分和最大得分.

算法设计: 对于给定n堆石子, 计算合并成一堆的最小得分和最大得分.

数据输入: 第1行是正整数n, 1<=n<=100, 表示有n堆石子. 第2行有n个数, 分别表示n堆石子的个数.

结果输出: 第1行是最小得分, 第2行是最大得分.






















  测试输入 期待的输出 时间限制 内存限制 额外进程
测试用例 1  

  1. 36↵

  2. 53 49 2 9 9 30 2 35 1 46 39 46 42 33 13 41 35 57 38 59 15 40 18 6 46 30 53 31 34 57 41 20 1 42 59 46 45 ↵

 以文本方式显示

  1. 5913↵

  2. 24595↵

 1秒 64M 0

上面我们只讨论了最小的情况，本题需要将最大、最小情况输出。其实最大、最小的套路是一摸一样的，只是在比较的时候改变一下符号而已。且：在求最大的情况下，上面针对求最小时的四边形不等式的优化不可用，需要老老实实遍历。

直接附上AC代码：

  1. //
  2. // Created by A on 2020/3/20.
  3. //
  4. #include <cstdio>
  5. #include <cmath>
  6. #include <climits>
  7. #include <algorithm>
  9. #define MAX 300
  11. using namespace std;
  12. /* 合并石子问题：环形排列着N堆石子，现在要将石子合并成一堆。
  13.  * 规定如下：每次只能将相邻的两堆石子合并，合并两堆石子所花费的时间为两堆石子的数量和。
  14.  * 求将N堆石子合并成一堆最小花费的时间。（石子分为n堆，石子的数量存储在数组p[0..n-1]中）*/
  16. // 改进版2！！！！！
  17. int min_ans[2 * MAX][2 * MAX] = {0};
  18. int max_ans[2 * MAX][2 * MAX] = {0};
  19. int min_divide[2 * MAX][2 * MAX] = {0};
  20. int max_divide[2 * MAX][2 * MAX] = {0};
  23. /* 将环形的石子化为线形 */
  24. void GetList(int p[], int n) {
  25.     int j = 0;
  26.     for (int i = n; i < 2 * n - 1; i++)
  27.         p[i] = p[j++];
  28. }
  30. void initDivideArray(int n) {
  31.     for (int i = 0; i < n; i++) {
  32.         min_divide[i][i] = i;
  33.         max_divide[i][i] = i;
  34.     }
  36. }
  38. void MergeStone(int p[], int n) {
  40.     GetList(p, n);  //化圆为直
  41.     int N = 2 * n - 1;// 线形中石子堆个数看做 2n - 1
  42.     initDivideArray(N);  //初始化divide数组
  44.     /* 石子堆的个数：从1到n */
  45.     for (int l = 2; l <= n; l++) {
  46.         /* 讨论l个石子的石子堆 p[i..j] */
  47.         for (int i = 0; i < N - l + 1; i++) {
  48.             int j = i + l - 1;
  49.             /* 计算石子堆p[i..j]的总数 */
  50.             int sum = 0;
  51.             for (int t = i; t <= j; t++)
  52.                 sum += p[t];
  54.             /* 依次讨论每一个分割点d:将石子堆p[i..j]分成p[i..k]和 A[k+1..j] */
  55.             min_ans[i][j] = INT_MAX;
  56.             for (int temp, k = min_divide[i][j - 1]; k <= min_divide[i + 1][j]; k++) {
  57.                 temp = min_ans[i][k] + min_ans[k + 1][j] + sum;
  58.                 if (temp < min_ans[i][j]) {
  59.                     min_ans[i][j] = temp;
  60.                     min_divide[i][j] = k;
  61.                 }
  62.             }
  63.             max_ans[i][j] = INT_MIN;
  64.             for (int temp, k = i; k < j; k++) {
  65.                 temp = max_ans[i][k] + max_ans[k + 1][j] + sum;
  66.                 if (temp > max_ans[i][j]) {
  67.                     max_ans[i][j] = temp;
  68.                     max_divide[i][j] = k;
  69.                 }
  70.             }
  71.         }
  72.     }
  73. }
  75. int main() {
  76.     int n, p[MAX];
  77.     scanf("%d", &n);
  78.     for (int i = 0; i < n; i++)
  79.         scanf("%d", &p[i]);
  81.     MergeStone(p, n);
  82.     int maxResult = INT_MIN, minResult = INT_MAX;
  83.     for (int i = 0, j = n - 1; i < n; i++, j++) {
  84.         maxResult = max(maxResult, max_ans[i][j]);
  85.         minResult = min(minResult, min_ans[i][j]);
  86.     }
  87.     printf("%d\n%d\n", minResult, maxResult);
  88. }

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80Mzc4NzA0Mw_size_16_color_FFFFFF_t_70 2

有任何问题欢迎评论交流，如果本文对您有帮助不妨点点赞，嘻嘻~

end

欢迎关注个人公众号“ 鸡翅编程 ”，这里是认真且乖巧的码农一枚。

—— 做最乖巧的博客er，做最扎实的程序员 ——

旨在用心写好每一篇文章，平常会把笔记汇总成推送更新~

在这里插入图片描述

发表评论

表情：
评论列表 （有 0 条评论，150人围观）

还没有评论，来说两句吧...

相关阅读

    相关 石子合并问题 （区间dp）

    石子合并问题是最经典的DP问题。首先它有如下3种题型： (1)有N堆石子，现要将石子有序的合并成一堆，规定如下：每次只能移动任意的2堆石子合并，合并花费为新合成的

    叁歲伎倆叁歲伎倆/ 0 赞/ 304 阅读

    相关 282 石子合并（区间dp）

    1. 问题描述： 设有 N 堆石子排成一排，其编号为 1，2，3，…，N。每堆石子有一定的质量，可以用一个整数来描述，现在要将这 N 堆石子合并成为一堆。每次只能合并相邻的两

    朱雀朱雀/ 0 赞/ 334 阅读