282 石子合并（区间dp）-蒲公英云

282 石子合并（区间dp）

朱雀 2022-09-12 12:49 306阅读 0赞

1. 问题描述：

设有 N 堆石子排成一排，其编号为 1，2，3，…，N。每堆石子有一定的质量，可以用一个整数来描述，现在要将这 N 堆石子合并成为一堆。每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同。
例如有 4 堆石子分别为 1 3 5 2，我们可以先合并 1、2 堆，代价为 4，得到 4 5 2，又合并 1，2 堆，代价为 9，得到 9 2 ，再合并得到 11，总代价为 4+9+11=24；如果第二步是先合并 2，3 堆，则代价为 7，得到 4 7，最后一次合并代价为 11，总代价为 4+7+11=22。问题是：找出一种合理的方法，使总的代价最小，输出最小代价。

输入格式

第一行一个数 N 表示石子的堆数 N。第二行 N 个数，表示每堆石子的质量(均不超过 1000)。

输出格式

输出一个整数，表示最小代价。

数据范围

1 ≤ N ≤ 300

输入样例：

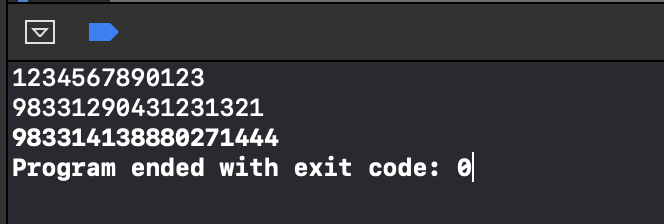
4
1 3 5 2

输出样例：

22
来源：https://www.acwing.com/problem/content/description/284/

2. 思路分析：

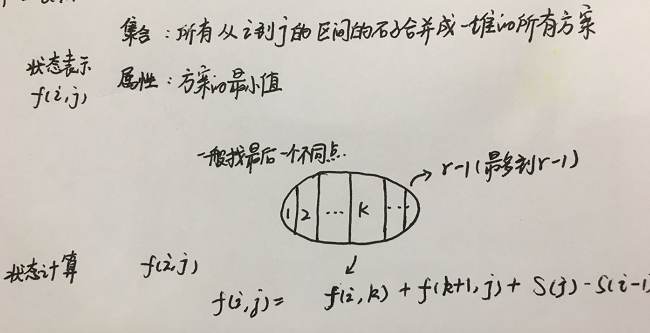
这道题目属于区间dp入门的经典题目，对于区间dp问题一般问的是”合并相邻的区间…求解花费的最小代价…”，主要的思路是每一次求解所有以当前起点开始的长度为l的区间最值，这样最终的dp[1][n]就是答案，所以对于区间dp的问题一般需要声明两维。对于动态规划的问题一般需要分为两个步骤处理：① 状态表示；② 状态计算；根据前面的分析可以知道我们可以声明一个二维数组，其中dp[i][j]表示所有从i到j的区间的石子合并为一堆石子的集合的最小花费，；状态计算其实也比较容易想，一般是找最后一个不同点，因为最终是将区间中的两堆石子合并为一堆石子，所以我们可以根据当前区间划分为两个区间的分界点来枚举，枚举所有将当前区间合并为一个区间的分界点，计算划分的每一个集合的最大值即可，最终dp[1][n]表示的就是区间[1: n]合并所有石子的最小花费。区间dp都有基本的套路，一般使用三层循环枚举，第一层循环枚举长度l，第二层循环枚举起点i，第三层循环枚举起点为i，终点为j的区间的分界点，计算将当前区间划分为若干个的集合之后求解每一个集合的最小花费。

watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBAeXV6aGFuZ196eQ_size_19_color_FFFFFF_t_70_g_se_x_16

3. 代码如下：

if __name__ == '__main__':
    n = int(input())
    a = list(map(int, input().split()))
    dp = [[0] * (n + 2) for i in range(n + 2)]
    INF = 10 ** 9
    # 前缀和, 下标从1开始这样会比较好处理
    s = [0]
    for i in range(1, n + 1):
        s.append(s[-1] + a[i - 1])
    for l in range(2, n + 1):
        i = 1
        # 注意边界
        while i + l - 1 <= n:
            j = i + l - 1
            # 当前区间的应该置为最大值
            dp[i][j] = INF
            # 依据当前区间划分为两个区间的分界点进行划分
            for k in range(i, j):
                dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + s[j] - s[i - 1])
            i += 1
    print(dp[1][n])