数字三角形模型 AcWing 1027. 方格取数-蒲公英云

数字三角形模型 AcWing 1027. 方格取数

原题链接

AcWing 1027. 方格取数

算法标签

DP 线性DP

思路

错误思路：分两次走

由于第一次走时可能存在多条路径都是第一次的解集，分开走只能选择其中的一条。但第一次走过的地方会被重置成0，无法确定是第一次同样是最优解而未被你选择的情况下第二次的值会不会比你已经得出的答案要大
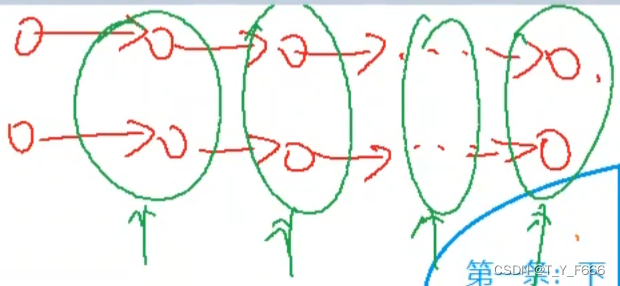
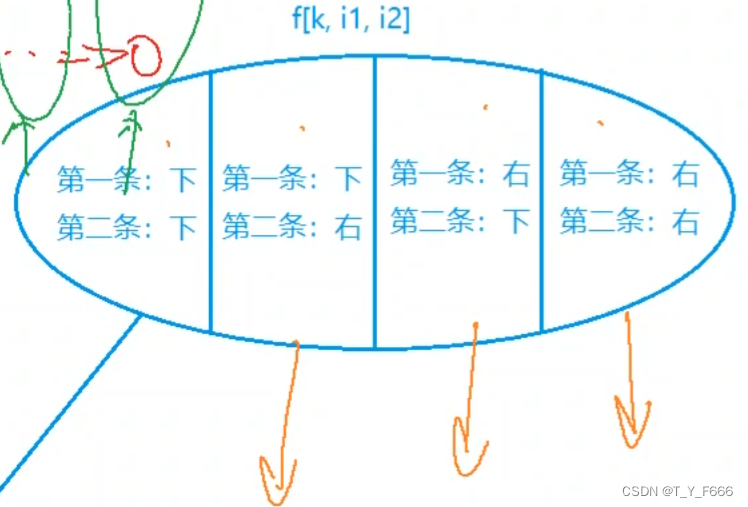
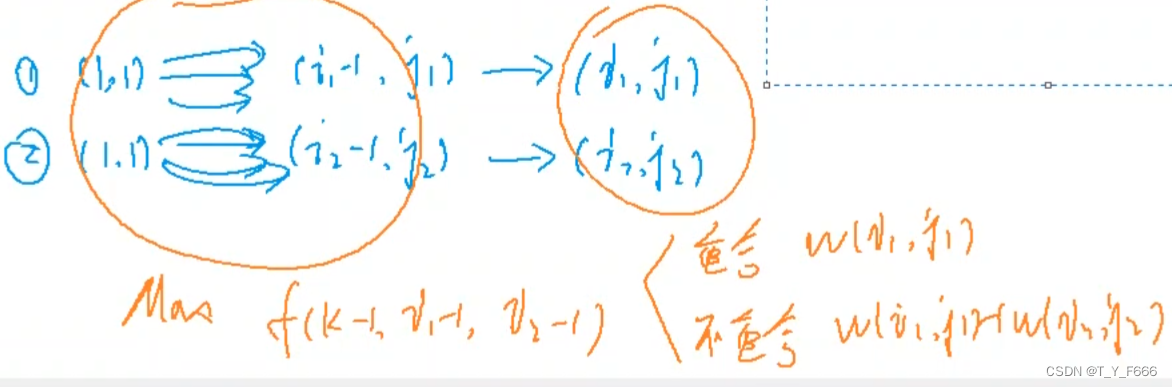
在这里插入图片描述

代码

#include<bits/stdc++.h>
#define int long long
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
const int N = 105;
int f[2*N][N][N], a[N][N];
int aa, b, c, d;
inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
void put(int x) {
    if(x<0) putchar('-'),x=-x;
    if(x>=10) put(x/10);
    putchar(x%10^48);
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n=read();
    while(aa=read(), b=read(), c=read(), aa||b||c){
        a[aa][b]=c;
    }
    // 行列值之和 由行确定列
    rep(k, 2, n+n+1){
        // 第一次第i行
        rep(i1, 1, n+1){
            // 第二次第i行
            rep(i2, 1, n+1){
                // j1表示第一次第j列 j2表示第二次第j列
                int j1=k-i1, j2=k-i2;
                if(j1>=1&&j1<=n&&j2>=1&&j2<=n){
                    int t=a[i1][j1];
                    // 非同一条路径
                    if(i1-i2){
                        t+=a[i2][j2];
                    }
                    // 下下 下右 右下 右右
                    f[k][i1][i2]=max({f[k][i1][i2], f[k-1][i1-1][i2-1]+t, f[k-1][i1-1][i2]+t, f[k-1][i1][i2-1]+t, f[k-1][i1][i2]+t});
                }
            }
        } 
    }
    printf("%lld", f[2*n][n][n]);
    return 0;
}