洛谷——P1548 [NOIP1997 普及组] 棋盘问题-蒲公英云

洛谷——P1548 [NOIP1997 普及组] 棋盘问题

矫情吗；* 2023-10-02 11:24 114阅读 0赞

P1548 [NOIP1997 普及组] 棋盘问题

题目描述

设有一个N \times MN×M方格的棋盘(1≤N≤100,1≤M≤100)(1≤N≤100,1≤M≤100)

求出该棋盘中包含有多少个正方形、多少个长方形（不包括正方形）。

例如：当 N=2, M=3N=2,M=3时：

正方形的个数有88个：即边长为11的正方形有66个；

边长为22的正方形有22个。

长方形的个数有1010个：

即

2 \times 12×1的长方形有44个

1 \times 21×2的长方形有33个：

3 \times 13×1的长方形有22个：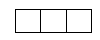

3 \times 23×2的长方形有11个：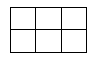

如上例：输入：2,32,3

输出：8,108,10

输入格式

N,MN,M

输出格式

正方形的个数与长方形的个数

输入输出样例

输入 #1复制

2 3

输出 #1复制

8 10

说明/提示

【题目来源】

NOIP 1997 普及组第一题

#include<bits/stdc++.h>
#include<algorithm>
using namespace std; 
int main(){
    int n,m,z=0,c=0,x,y;
    cin>>n>>m;
    for(int i=0;i<=n;i++){
        for(int j=0;j<=m;j++){
            for(x=i+1;x<=n;x++){
                for(y=j+1;y<=m;y++){
                    if(x-i==y-j) z++;
                    else c++;
                }
            }
        }
    } 
    cout<<z<<" "<<c;
    return 0;
}