什么是一阶矩和二阶矩？
期望的公式扩展
一阶矩就是期望值，换句话说就是平均数(离散随机变量很好理解，连续的可以类比一下)。举例：xy坐标系中，x取大于零的整数，y1, y2, …,yn 对应x=1, 2,…, n的值，现在我要对y求期望，就是所有y累加除以n，也就是y的均值。
此时y的均值我可以在坐标系中画一条线，我会发现所有的点都在这条线的两边。如果是中心矩我就会用每个值减去均值z=yn-y均作为一个新的序列z1, z2, …, zn，再对z求期望，这时我会发现均值为零(即在坐标轴y上)。一阶矩只有一阶非中心矩，因为一阶中心矩永远等于零。
二阶(非中心)矩就是对变量的平方求期望，二阶中心矩就是对随机变量与均值(期望)的差的平方求期望。为什么要用平方，因为如果序列中有负数就会产生较大波动，而平方运算就好像对序列添加了绝对值，这样更能体现偏离均值的范围。
向左转|向右转
扩展资料：
在数理统计学中有一类数字特征称为矩。
原点矩：令k为正整数（或为0），a为任何实数，X为随机变量，则期望值
向左转|向右转
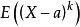
叫做随机变量X对a的k阶矩，或叫动差。如果a=0，则有E（X^k），叫做k阶原点矩，记作
向左转|向右转
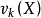，也叫k阶矩。
向左转|向右转
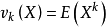
显然，一阶原点矩就是数学期望，即
向左转|向右转
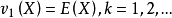
原点矩顾名思义，是随机变量到原点的距离（这里假设原点为零点）。中心矩则类似于方差，先要得出样本的期望即均值，然后计算出随机变量到样本均值的一种距离，与方差不同的是，这里所说的距离不再是平方就能构建出来的，而是k次方。
这也就不难理解为什么原点矩和中心矩不是距离的“距”，而是矩阵的“矩”了。我们都知道方差源于勾股定理，这就不难理解原点矩和中心矩了。还能联想到力学中的力矩也是“矩”，而不是“距”。力矩在物理学里是指作用力使物体绕着转动轴或支点转动的趋向。力矩也是矢量，它等于力乘力臂。
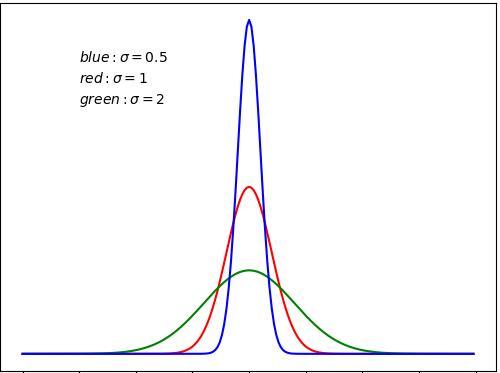
二阶中心矩，也叫作方差，它告诉我们一个随机变量在它均值附近波动的大小，方差越大，波动性越大。方差也相当于机械运动中以重心为转轴的转动惯量。三阶中心矩告诉我们一个随机密度函数向左或向右偏斜的程度。
在均值不为零的情况下，原点矩只有纯数学意义。
转载于
//www.cnblogs.com/jfdwd/p/11239101.html
た 入场券
àì夳堔傛蜴生んèń
爱被打了一巴掌
￡神魔★判官ぃ
还没有评论，来说两句吧...