ACM DP 石子合并问题

小灰灰 2022-06-10 01:17 306阅读 0赞

滴，集训第二十一天打卡。

可能是对组队不太满意，都不大高兴做新的训练…

所以最近一直在磨DP，翻一下博客，发现最近都是DP啊…

这个石子合并的，我做的训练数据n是40000直线型的，一开始没注意，先做了环形，再换直线，然后发现朴素DP不能用了…

再看的GarsiaWachs算法，一上午啊，都在这了..

部分参考来自http://blog.csdn.net/acdreamers/article/details/18039073

石子合并有三种题型。

(1)有N堆石子，现要将石子有序的合并成一堆，规定如下：每次只能移动任意的2堆石子合并，合并花费为新合成的一堆石子的数量。求将这N堆石子合并成一堆的总花费最小（或最大）。

分析：当然这种情况是最简单的情况，合并的是任意两堆，直接贪心即可，每次选择最小的两堆合并。本问题实际上就是哈夫曼的变形。

(2)有N堆石子，现要将石子有序的合并成一堆，规定如下：每次只能移动相邻的2堆石子合并，合并花费为新合成的一堆石子的数量。求将这N堆石子合并成一堆的总花费最小（或最大）。

分析：我们熟悉矩阵连乘，知道矩阵连乘也是每次合并相邻的两个矩阵，那么石子合并可以用矩阵连乘的方式来解决。

设dp[i][j]表示第i到第j堆石子合并的最优值，sum[i][j]表示第i到第j堆石子的总数量。那么就有状态转移公式：

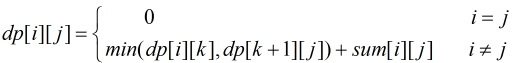
20140109140456093

最普通的算法O(n^3)：

其中，dp[i][j]代表i到j堆的最优值，sum[i]代表第1堆到第i堆的数目总和。

  1. #include <stdio.h>
  2. #include <algorithm>
  3. using namespace std;
  4. int dp[205][205],sum[205],a[205];
  5. int main()
  6. {
  7.     int n,i,j,k,l,s;
  8.     while(scanf("%d",&n)!=EOF)
  9.     {
  10.         s=0;
  11.            for(i=1;i<=n;i++)
  12.         {
  13.             scanf("%d",&a[i]);
  14.             s+=a[i];
  15.             sum[i]=s;
  16.         }
  17.            //memset(dp,0,sizeof(dp));
  18.            for(i=1;i<=n;i++)
  19.         dp[i][i]=0;
  20.            for(l=1;l<n;l++)
  21.            {
  22.              for(i=1;i<=n-l;i++)
  23.              {
  24.                 j=i+l;
  25.                 dp[i][j]=1000000000;
  26.                 for(k=i;k<=j;k++)
  27.                 dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);
  28.                 dp[i][j]+=sum[j]-sum[i-1];
  29.              }      
  30.           }
  31.         printf("%d\n",dp[1][n]);
  32.     }
  33. }

考虑四边形不等式优化，接近O(n^2)：

原状态转移方程中的k的枚举范围便可以从原来的(i~j-1)变为(s[i,j-1]~s[i+1,j])。

  1. #include <stdio.h>
  2. #include <algorithm>
  3. using namespace std;
  4. int dp[105][105],sum[105],a[105],ss[105][105];
  5. int main()
  6. {
  7.     int n,i,j,k,l,s;
  8.     while(scanf("%d",&n)!=EOF)
  9.     {
  10.            s=0;
  11.            for(i=1;i<=n;i++)
  12.         {
  13.             scanf("%d",&a[i]);
  14.             s+=a[i];
  15.             sum[i]=s;
  16.         }
  17.         //memset(dp,0,sizeof(dp));
  18.         for(i=1;i<=n;i++)
  19.         dp[i][i]=0,ss[i][i]=i;
  20.         for(l=1;l<n;l++)
  21.         {
  22.              for(i=1;i<=n-l;i++)
  23.              {
  24.                 j=i+l;
  25.                 dp[i][j]=1000000000;
  26.                 for(k=ss[i][j-1];k<=ss[i+1][j];k++)
  27.                  {
  28.                      if(dp[i][j]>dp[i][k]+dp[k+1][j])
  29.                     {
  30.                         dp[i][j]=dp[i][k]+dp[k+1][j];
  31.                         ss[i][j]=k;
  32.                     }
  33.                  }
  34.                 dp[i][j]+=sum[j]-sum[i-1];
  35.             }      
  36.         }
  37.         printf("%d\n",dp[1][n]);
  38.     }    
  39. }

HYSBZ-3229 石子合并(GarsiaWachs算法)

在一个操场上摆放着一排N堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的2堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的得分。 试设计一个算法，计算出将N堆石子合并成一堆的最小得分。

Input

　　第一行是一个数N。
　　以下N行每行一个数A，表示石子数目。

Output

　　共一个数，即N堆石子合并成一堆的最小得分。

Sample Input

4

1

1

1

1

Sample Output

8

HINT

对于 100% 的数据，1≤N≤40000

对于 100% 的数据，1≤A≤200

思路：区间DP不能做了，范围40000开二维太大了。

  1. #include <stdio.h>
  2. int stone[40005],ans,t;
  3. void combine(int k)
  4. {
  5.     int tmp,i,j,d;
  6.     tmp=stone[k-1]+stone[k];
  7.     ans+=tmp;
  8.     t--;
  9.     for(i=k;i<t;i++) 
  10.     stone[i]=stone[i+1];
  11.     for(j=k-1;stone[j-1]<tmp;j--)
  12.     stone[j]=stone[j-1];
  13.     stone[j]=tmp;
  14.     while(j>=2&&stone[j]>=stone[j-2])
  15.     {
  16.         d=t-j;
  17.         combine(j-1);
  18.         j=t-d;
  19.     }
  20. }
  21. int main()
  22. {
  23.     int n,i,j;
  24.     scanf("%d",&n);
  25.     stone[0]=0x3f3f3f3f; 
  26.     stone[n+1]=0x3f3f3f3f-1;
  27.     for(i=1;i<=n;i++)
  28.     scanf("%d",&stone[i]);
  29.     ans=0;t=3;
  30.     for(i=3;i<=n+1;i++)
  31.     {
  32.         stone[t++]=stone[i];
  33.         while(stone[t-3]<=stone[t-1])
  34.         combine(t-2);
  35.     }
  36.     while(t>3) 
  37.     combine(t-1);
  38.     printf("%d\n",ans);
  39.     return 0;
  40. }

(3)问题(2)的是在石子排列是直线情况下的解法，如果把石子改为环形排列，又怎么做呢？

分析：状态转移方程为：

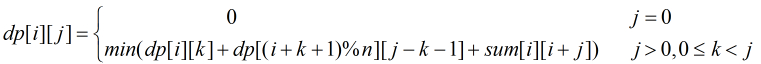
20140109151455062

其中有：

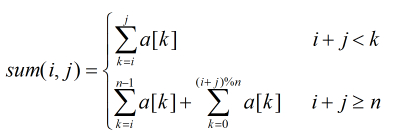
20140109151533250

  1. #include <stdio.h>
  2. #include <string.h>
  3. #include <algorithm>
  4. using namespace std;
  5. int dp[1005][1005];
  6. int main()
  7. {
  8.     int n,i,j,a[1001],sum[1005],s=0,k,l;
  9.     scanf("%d",&n);
  10.     sum[0]=0;
  11.     for(i=1;i<=n;i++)
  12.     {
  13.         scanf("%d",&a[i]);
  14.         s+=a[i];
  15.         sum[i]=s;
  16.     }
  17.     memset(dp,0,sizeof(dp));
  18.     for(l=2;l<=n;l++)//归并的石子长度
  19.     {
  20.         for(i=1;i<=n-l+1;i++)//i为起点，j为终点
  21.         {
  22.             j=i+l-1;
  23.             dp[i][j]=1000000000;
  24.             for(k=i;k<=j;k++)
  25.             dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]);
  26.         }
  27.     }
  28.     printf("%d\n",dp[1][n]);
  29. }

发表评论

表情：
评论列表 （有 0 条评论，306人围观）

还没有评论，来说两句吧...

相关阅读

    相关 石子合并问题 （区间dp）

    石子合并问题是最经典的DP问题。首先它有如下3种题型： (1)有N堆石子，现要将石子有序的合并成一堆，规定如下：每次只能移动任意的2堆石子合并，合并花费为新合成的

    叁歲伎倆叁歲伎倆/ 0 赞/ 305 阅读

    相关 282 石子合并（区间dp）

    1. 问题描述： 设有 N 堆石子排成一排，其编号为 1，2，3，…，N。每堆石子有一定的质量，可以用一个整数来描述，现在要将这 N 堆石子合并成为一堆。每次只能合并相邻的两

    朱雀朱雀/ 0 赞/ 336 阅读

    相关 石子合并问题

    在一个圆形操场的四周摆放着n堆石子。现要将石子有次序地合并成一堆。规定每次只能选择相邻的两堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的得分。试设计一个算法，计算出将n

    傷城~傷城~/ 0 赞/ 316 阅读

    相关 ACM DP 石子合并问题

    滴，集训第二十一天打卡。 可能是对组队不太满意，都不大高兴做新的训练... 所以最近一直在磨DP，翻一下博客，发现最近都是DP啊... 这个石子合并的，我做的训练数据n是

    小灰灰小灰灰/ 0 赞/ 307 阅读