方格取数（动态规划经典题）-蒲公英云

方格取数（动态规划经典题）

墨蓝 2022-06-10 05:18 335阅读 0赞

描述

设有N*N的方格图(N<=10),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字0。如下图所示（见样例）：< p=””>

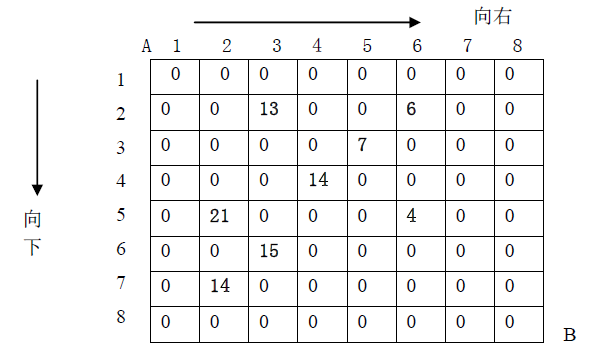
某人从图的左上角的A 点出发，可以向下行走，也可以向右走，直到到达右下角的B点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。此人从A点到B 点共走两次，试找出2条这样的路径，使得取得的数之和为最大。

输入

输入的第一行为一个整数N（表示N*N的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的0表示输入结束。

输出

只需输出一个整数，表示2条路径上取得的最大的和。

样例输入

样例输出

来源

NOIP2000复赛提高组第四题

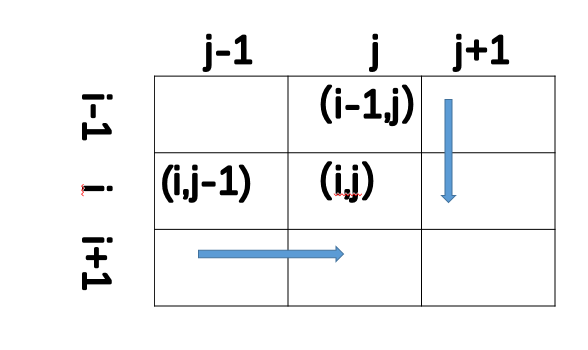
20170810210823678

设状态：f[i][j][h][k];//表示两条路同时走，第一条路径走到(i,j)时，第二条走到（h,k）时的最大数字和；
初始状态：f[0][0][0][0]=0;

最终状态：f[n][n][n][n];

状态转移方程：当i==h&&j==k时，f[i][j][h][k]=max{f[i-1][j][h-1][k],f[i][j-1][h][k-1],f[i-1][j][h][k-1],f[i][j-1][h-1][k])+a[i][j];//取上上，左左，上左，左上四个方向的最大值加上当前的值；

当i!=h&&j!=k时，f[i][j][h][k]=max{f[i-1][j][h-1][k],f[i][j-1][h][k-1],f[i-1][j][h][k-1],f[i][j-1][h-1][k])+a[i][j]+a[h][k];//取上上，左左，上左，左上四个方向的最大值加上两条路径当前的值；

/*
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
*/
#include<iostream>
using namespace std;
int f[51][51][51][51];//f[i][j][h][k]表示第一条路径走到第（i，j）点，第二条路径走到第(h,k)点时最大数字和
int a[51][51];//存储方格中的数，例如2 3 13,表示a[2][3]=13; 
int n,i,j,h,k,x,y,z;
int main()
{
    cin>>n;
    while(cin>>x>>y>>z)//输入数据 
    {
        if(x==0&&y==0&&z==0) break;
        a[x][y]=z;
    } 
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=n;j++)
        {
            for(h=1;h<=n;h++)
            {
                for(k=1;k<=n;k++)
                {
                    int tmp1=max(f[i-1][j][h-1][k],f[i][j-1][h][k-1]);//上上、左左两个方向
                    int tmp2=max(f[i][j-1][h-1][k],f[i-1][j][h][k-1]);//左上、上左两个方向 
                    f[i][j][h][k]=max(tmp1,tmp2)+a[i][j];
                    if(i!=h&&j!=k) f[i][j][h][k]+=a[h][k];
                }
            }
        }
    }
    cout<<f[n][n][n][n]<<endl;
    return 0;
}